The margin of error calculator could be an applied math knowledge wont to indicate the number of sampling errors within the survey results.
What Is the Margin Of Error Calculator?
The margin of error calculator is how many percentage points your result differs from the overall actual value. For example, a 95% confidence interval and a 4% margin of error mean that your statistics are within 4 percentage points of the true population value. 95% of the time. From a technical point of view, the error rate is the range of values below and above the sample statistical value within the confidence interval.
Confidence interval is a way to show how high the uncertainty of a given statistical data is (for example, it can be shown from the survey that the 98% confidence interval is 4.88 and 5. 26, that is, if the same method is used to repeat the survey of 98% of the actual population The time when the parameter (parameter or statistic) falls within the interval estimate (between 4.88 and 5.26 in 98% of cases).
The idea behind trust and margin of error is that the difference between each poll and the actual population is certain. However, the confidence interval and the error limit reflect the fact of the error range. Although a 95% or 98% confidence interval and a 2% margin of error seem to be a good statistic, the margin of error is built-in, which means that sometimes the statistics are wrong. For example, a 2012 Gallup poll found (incorrectly) that Romney would win the 2012 election with 49% Romney and 48% Obama. The reported confidence is 95% and the uncertainty is +/- 2, which means that 95% of the time the accuracy of the calculation result is 2 percentage points. The actual election results are as follows: Obama-51%, Romney-47%, actually exceeded the error range of the Gallup poll (2%), which shows that not only the statistics may be wrong, but also the polls. it’s wrong.
How to Calculate in Margin of Error Calculator?

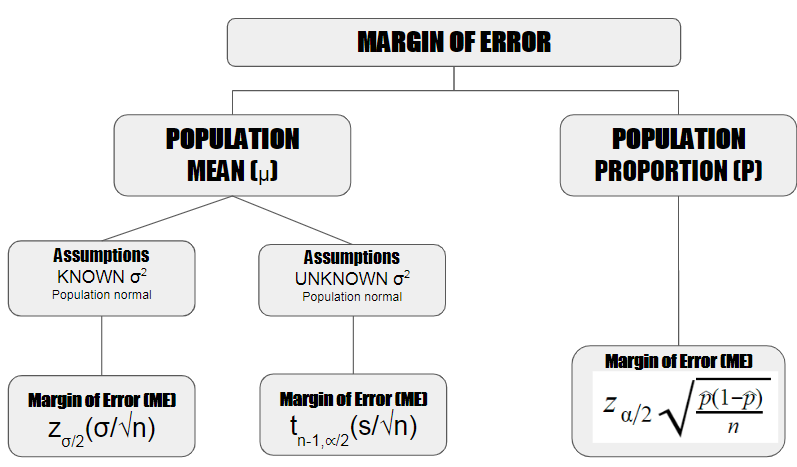
The margin of error represents the variety of values above and below the arrogance interval. Still don’t perceive visiting Chegg.com; they’ll prepare a period counselor for you, and your initial half-hour is free! Associate in Nursing canvass showed that a selected candidate won the election with 51% of the vote. the arrogance level is 95% and also the error is 4%. For example, suppose an equivalent methodology is employed to repeat the survey. Sociologists predict that 95% of the time, the result are going to be inside 4% of the prescribed result (51%). In alternative words, 95% of the time they assume the result’s between fifty one-4 = four7% and 51 + 4 = 55%. There are 2 ways to calculate the error rate, betting on whether or not you’re overall statistics or sample statistics: Error limit = crucial worth x overall normal deviation. Error limit = critical value x standard sampling error.
How to calculate uncertainty: Step
Step 1: Find the critical value. The critical value is the T score or Z score. If you are not sure, please refer to the T score and Z score. For small sample sizes (less than 30) or when you do not know the population standard deviation, use the t-score. Otherwise, use the z index. Click here to watch a one-minute video showing how to determine the threshold.
Step 2: Find the standard deviation or standard error. They are the same, but you need to know the parameters of the population to calculate the standard deviation. Otherwise, calculate the standard error (see: What is the standard error? Click here to watch a short video on how to calculate the standard error.
Step 3: Multiply the critical value of step 1 by the standard deviation or standard error of step 2. For example, if your resume is 1.95 and SE is 0.019, then 95 * 0.019 = 0.03705.
Example question: 900 students were interviewed, and their average grade was 2.7 and the standard deviation was 0. Calculate the margin of error for 90% confidence: the critical value is 1.645 (see this video for calculations). Derived from the question), but since this is a sample, we need the standard error of the mean. The formula for the SE average is standard deviation/√ (sample size), so: 0.4 /√(900) = 0.013.645 * 0.013 = 0.021385 This is how the error rate is calculated! Back to the top of the
Error Rate of Proportion:
The formula of proportion is slightly different:
where: = sample proportion (“P-hat”), n = sample size, z = z score.
Example question : A thousand humans had been surveyed and 380 notions that weather alternate became now no longer because of human pollution. Find the MoE for a 90% self-belief c programming language.
Step 1: Find P-hat via way of means of dividing the number of individuals who replied positively. “Positively” on this experience doesn’t suggest that they gave a “Yes” answer; It way that they replied in step with the announcement withinside the question. In this case, 380/a thousand humans (38%) replied positively.
Step 2: Find the z-rating that is going with the given self-belief c programming language. You’ll want to reference this chart of not unusual place essential values. A 90% self-belief c programming language has a z-rating (an essential value) of 1.645.
Step 3 : Insert the values into the components and solve: = 1.645 * 0.0153 = 0.0252
Step 4: Turn Step three right into a percentage: 0.0252 = 2.52% The margin of mistakes is 2.52%.
Concept of Margin of Error Calculator:
Think of a simple “yes/no” survey as a sample of respondents from the population who reported a positive response. We want to know how close you are to the true results of the entire population survey without having to do so. If we want to investigate subsequent samples of respondents (sample only), we can assume that these subsequent results are normally distributed. The margin of error describes the distance expected for a certain percentage change in these results. According to rule 68-95-99.7, we expect that 95% of the result {\ display style p_ {1}, p_ {2}, \ldots} will be within about two standard deviations ({\ display style \ pm 2 \ sigma_ {P } ). }) The true mean of both sides {\ display style {\ overline {p}}}. This interval is called the confidence interval, and the radius (half of the interval) is called the error tolerance, which is 95% confidence. Level ce {\ display style \ gamma}, the sample size {\ displaystyle n} comes from the population with the expected standard deviation {\ display style \ sigma}, and its error rate {\ display style MOE _ {\ gamma} = z _ {\ gamma} \ times {\ sqrt {\ frac {\ sigma ^ {2}} {n}, where {\ display style z _ {\ gamma}} represents the quantile (usually also az), and {\ display style {\ sqrt {\ frac {\ sigma ^ {2}} {n}}}-standard error.
SUMMARY: In the confidence interval, the range of values above and below the sample statistic is called the margin of error calculator range. For example, suppose we want to know the percentage of adults who exercise every day. We can design a sample to ensure that our sample estimate does not differ by more than 5% (error rate) from 90% of the time (confidence level) of the actual population.
To Calculate the Margin of Error:
You can find the margin of error using one of the following formulas: margin of error = critical value x statistical standard deviation. Error limit = critical value x standard error of statistics. Statistical standard deviation, use the first equation to calculate the error. Otherwise, use the second equation. Earlier we described how to calculate the standard deviation and standard error.’
Finding the Essential value:
The critical value may be an issue accustomed calculate uncertainty. This section describes the way to find the critical value once the statistical distribution of applied math information is normal or getting ready to normal. If the distribution of the sample is close to a standard distribution, the critical value may be expressed as a t-score or z-score. Follow the steps below to seek out the critical value:
1: Calculate alpha (α): α = 1-(confidence degree / 100)
2: realize the critical likelihood value (p *): p * = 1-α/ 2
3: to precise the critical value is that the z-score, find the z-score with the additive likelihood equivalent to the essential probability (p*).
4: to point the critical price in datums, do the following:
5: realize the degree of freedom (DF) once estimating the common or proportion of the sample, DF is that the sample size minus one. Freedom may be calculated in many ways. We can describe these calculations as they appear.
6: The critical t statistic (t *) is the t statistic with the degree of freedom adequate to DF and also the cumulative probability equal to the critical probability (p *).
Should T-score and Z-score Critical Values be Expressed as T Statistic or Z-score?
One way to answer this question is based on the standard deviation of the population:
- If the population standard deviation is known, use the z-score.
- If the population standard deviation is unknown, the t statistic is used.
Another approach focuses on sample size.
- If the sample size is large, use the z-score (the central limit theorem provides a useful basis for determining whether the sample is “large”).
- If the sample size is small, please use the t statistic.
In practice, researchers can use the above suggestions in combination. When the population standard deviation is known and the sample size is large, we use the z-score on this website. Otherwise, when the sample size is small and the underlying distribution is abnormal, we will use the t statistic.
Calculating the Margin of Error of the Sample Mean :
When a research question requires you to determine the statistical mean (or mean) of the sample, you must provide the margin of error (MOE) of the sample mean. The error rate of the sample proportion, that is, the comparison of the “hit number” in the sample with the total number. The general formula for the error range of the sample mean (assuming certain conditions are met, see below) is the population standard deviation, n is the number of samples, and z* is the corresponding z* value. For the required confidence level (can be found in the table below).
Please note that these prices are taken from the quality Gaussian distribution (Z-). the world between any z* value and negative z* value is that the confidence proportion (approximate value). For example, the area between z * = 1.28 and z = -1.28 is close to 0.80. The chart may also be swollen to incorporate alternative confidence percentages. The graph solely shows the foremost ordinarily used confidence percentages.
The margin of Error and Sample Size Calculator:
The deviation is an estimate of the distance between the actual population value and the collected sample data. It is usually expressed as a percentage and depends on the size of the target market, sample size, and confidence. In short, you want the smallest flaws with the greatest possible confidence. In theory, if you can interview everyone in the population, you can eliminate bias and get 100% confidence because the sample size is equal to the population size. Since real-world online surveys deal with sample sizes ranging from a few hundred to a few thousand, the error calculator is used to determine the correct expectations and make decisions to determine how many respondents you need.
Population size (your target market):
Enter the number of people who theoretically belong to your target population. For example, if your survey is for adults in the United States, leave the default value at 250,000,000. To give a more restrictive example, if you only target K-5 teachers, please search for how many elementary school teachers in the country/region you are interested in, and then enter that number here.
Sample size:
Enter the number of responses for your budget. You can change it to run a hypothetical scenario and observe how the margin of error decreases as the number of samples increases. Generally, if you want to keep the margin of error at 5% or less and keep the confidence level at 95%, you want the sample size (also called N) to be greater than 400.
Confidence:
If you are not sure, please keep the confidence at the 95% industry standard. In short, this means that if you repeat the survey 100 times, that is, 100 repeats 95 times, the answer will be within a certain range. Error and 5 times are the biggest difference.
Error limit:
The error limit calculates how much the actual population value may differ from your sample response. For example, if you surveyed with a 5% error rate, and% of respondents said they knew more about your product, then you should explain in the following way: "40% to 50% of the population is interested to Learn more. As you can see, the margin of error works in both directions: +5% or -5% of the sample mean constitutes the so-called "confidence interval. Not sure where the real interest of the population in the entire region is because if you do the survey again, the answer will fluctuate slightly. Each time the error margin can predict the degree of such fluctuations. Finally, the deviation calculator provides a reliable statistical method that can predict the accuracy and reliability of the survey results compared with the general population. It is based on the assumption that you are using probability sampling methods. This means that all respondents in your survey will be randomly selected. The actual matching method may affect marginal estimates or errors or even make them unusable. We recommend that you consult an experienced statistician or market researcher. When in doubt.
SUMMARY: Error rate is statistical data that determines the percentage of survey results that may differ from the actual situation. In other words, this is a way of expressing the amount of random sampling error in the results. The confidence interval for this statistic. In essence, this can be regarded as a way to measure the effectiveness of the survey. The smaller the margin of error, the more likely your results will reflect the true position of the entire population, not just the sample. A useful statistical tool, when you understand its value, you can conduct more detailed research and safer methods.
How Do You Use The Margin Of Error Calculator?
To use the deviation calculator, do the following:
1: First, confirm whether or not to incorporate the ultimate population correction issue (FPC) within the calculation. ? As a general rule of thumb, calculate FPC once the sample size is 5 p.c or a lot of of the whole population. this is often vital as a result the sample size affects the metrics obtained from the data, love variance and standard. Difference from the example configuration.
2: Enter the number of samples, if mistreatment FPC calculation, enter the total number.
3: choose the required confidence level. The calculator uses it to find the corresponding z-score.
4:The very last thing you would like to try and do is to calculate the proportion of the sample (called p̂ or p-hat).To do this, please enter the number of individuals who gave answers that interest you.
For example, if a hundred people answered your survey and fifty-seven of them answered your question, please enter 57 during this field, and therefore the p worth is 0.57 (57/100). mistreatment of these values, the error calculator can offer you MOE immediately.
Using the uncertainty formula is an example:
et’s look at an example for clarification. Suppose we interviewed 400 people, which is equivalent to a population of 5,000 people. After getting the results, we noticed that 260 of them answered yes. Because we are very confident in the research, our confidence is 96%, because 400 is 8% of 5000 (please use the percentage calculator to check), we need to use the uncertainty formula including FPC.
Therefore, we use the following numbers:
1: Confidence = 96%, corresponding to a Z value of 2.05 (If you need more information about the Z value, please refer to the next paragraph).
2: z = 2.053
3: P = 50004
4: n = 4005
5: p̂ = 260/400 = 0.65
If you put the above value into the formula, you will get the following calculation result: The result shows that our data is within 4.69 percentage points of the actual population 96% of the time.
Conclusion:
The margin of error is arithmetical data and describes the number of random sampling mistakes in the review results. The greater the error, the more uncertain the results of the polls, which reflect the results of the polls of the entire population. Cannot be displayed completely and the result indicator has a positive variance (that is, indicator change), and the margin of error is positive. Deviations are usually used in non-survey environments and refer to observation errors in measurement reports. It is also used colloquially to indicate the scope or flexibility that may be required to achieve a certain goal. For example, commentators often use it in sports when describing the accuracy required for sports to reach goals. In the United States, the width of the bowling equipment used is 4.75 inches, so the width of the ball is 8.5 inches. Therefore, if the player tries to hit a fixed point to win, they will find a slip of 21.75 inches.
Frequently Asked Questions:
Q1: What is a great margin of mistake for a review?
A: The error rate used by most survey researchers is usually between 4% and 8%, with a confidence level of 95%.
Q2: How to calculate the 95% confidence interval?
A: To calculate the 95% confidence interval, first calculate the average and standard error: M = (2 + 3 + 5 + 6 + 9) / 5 = 5. Using the normal value becomes, you can find σM= = 1,118.95. Distribution calculator, and pointed out that the shaded area should be 0.95, and pointed out that the shaded area should be 0.95, and pointed out that the area should be between the intersections.
Q3: Are 10 errors allowed?
A: It depends on how the research is used. If it is a survey or census, the expected margin of error is very low. For most social science research, when trying to infer research trends or results, there is usually a 3-5% (sometimes as high as 10%) error rate.
Q4: How do you calculate the margin?
A: Divide gross profit by sales gross profit. To convert margins to percentages, multiply the result by 100. The margin is 25%.
Q5: What is a high error?
A: The error rate in statistics is the degree of error in randomly selected survey results. Big mistakes in the statistics indicate that the likelihood of trusting survey or opinion poll results is low, which means that the results are less reliable for representatives as a whole.
Q6: what’s the link between sample size and margin of error?
A: The link between error rate and the sample size is simple: the larger the sample size, the smaller the error. This relationship is termed backward as a result of they move within the opposite direction.
Q7: a way to calculate the net profit margin?
A: the proportion of the company’s gross profit is calculated by subtracting the worth of the products oversubscribed (COGS) from cyber web sales (total sales minus sales, bonuses, and discounts). Then divide that range by income to induce the gross margin.
Q8: what’s margin?
A: Example: Suppose you own stocks priced at $5,000 and purchase a further $5,000 margin, that is 50% of margin equity ($10,000 equity minus $5,000 margin). The stock fell to $6,000 and also the stock fell to $1,000 ($6,000 in inventory minus $5,000 in margin debt).
Question 9: What will the error rate tell us?
A: The margin of error may be an applied math knowledge that represents the number of sampling errors within the survey results. The larger the error, the less confidence that the survey results can mirror the survey results of the complete population.
Q10: What is a great gross interest margin?
A: You can ask: "What is a good victory? The good profit margins of various industries vary greatly, but in general, the net profit margin of 10% is considered to be medium, and the profit margin of 20% is considered high (or “Good”) while thinking that the 5% profit margin is low.