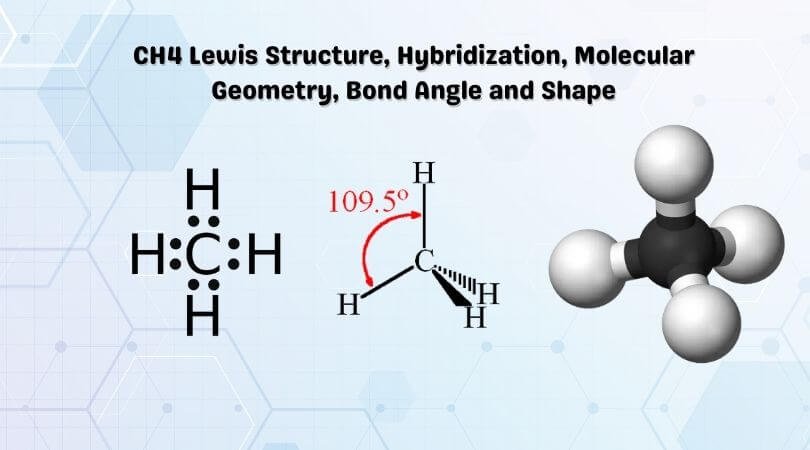
Ch4 Molecular Shape is Tetrahedral, four electron pairs are distributed in a tetrahedral shape. If these are all bond pairs the molecular geometry is tetrahedral. Discussing its properties, Methane is a drab and combustible gas. It is framed by the rotting of normal minerals and is generally utilized as fuel. CH4 is additionally utilized in the regular creation of a few natural mixtures.
The Shapes of Molecules
The synthetic holding in a compound is identified with its reactivity and properties – Na2O and H2O being very various materials. It is maybe more subtle that the state of an atom may likewise be vital to its physical and synthetic properties.
The fake sugar, aspartame, shows up very unique to sucrose (table sugar) yet gives a perspiration sensation in the mouth. Note these ‘stick’ constructions will be clarified in week 5.
CH4 Lewis Structure, Hybridization
Methane is one of the basic natural atoms, given its clear construction. It has the substance equation of CH4 and involves one carbon iota shaping bond with four hydrogen iotas.
-
The compound is one of the primary constituents of flammable gas. It is otherwise called an alkane.
-
Discussing its properties, Methane is a drab and combustible gas. It is framed by the rotting of normal minerals and is generally utilized as fuel.
CH4 is additionally utilized in the regular creation of a few natural mixtures.
Name of molecule Methane (CH4) No of Valence Electrons in the molecule 8 Hybridization of CH4 sp3 hybridization Bond Angles 109.5 degrees Molecular Geometry of CH4 Tetrahedral
In this blog entry, we will observe the Lewis Design, Sub-atomic Calculation, and State of the particle. In any case, before continuing with the Lewis Spot Design, we will initially view the all outnumber of valence electrons for this particle as these are the ones that partake in the bond development.
-
The electrons that take an interest in the bond development and are in the furthest shell of the iota are alluded to as valence electrons.
-
Absolute number of valence electrons for CH4 – Valence electrons of Carbon + Valence electrons of Hydrogen
Carbon has four valence electrons.
Every Hydrogen molecule has one valence electron, so there is an aggregate of four valence electrons for all Hydrogen iotas.
1. Absolute number of valence electrons for CH4 – 4 + 4 = 8
2. Consequently there are eight valence electrons for Methane.
Summary
Methane is a vapid and scentless gas framed from one iota of carbon and four particles of hydrogen having the compound recipe CH4. It is the least complex of soaked hydrocarbons. It is utilized for the age of power by consuming as a fuel in steam generator or gas turbine.
CH4 Lewis Structure
Lewis structure is the pictorial portrayal of the course of action of valence shell electrons in the particle, which assists us with understanding the iotas’ bond arrangements.
-
The electrons that take part in bond development are known as the holding pair of electrons, while those that don’t are known as nonbonding sets of electrons. Lewis structure is likewise alluded to as electron speck structure.
-
Specks are addressed to show the electrons, and lines are utilized to demonstrate the connections between the particles.
-
Lewis structures depend on the octet rule, which says a particle should have eight valence electrons in its external shell to accomplish a construction like the nearest honorable gas.
-
In this article, we will examine Methane (CH4) lewis spot structure, atomic math, electron calculation, hybridization, polar or nonpolar, its bond point, and so forth
-
Methane is primarily utilized as a fuel for turbines, water warmers, broilers, and so on It is likewise utilized in modern synthetic cycles to get ready different synthetic compounds.
Properties of Methane
It has a molar mass of 16.043 g/mol.
-
It has a limit of −161.5 °C and a liquefying point of −182.456 °C.
-
It is solvent in ethanol, ether, benzene, and so forth however insoluble in water.
-
It is a nontoxic and combustible gas.
Methane is effectively touched off.
Name of Molecule Methane Chemical formula CH4 Molecular geometry/shape of CH4 Tetrahedral Electron geometry of CH4 Tetrahedral Hybridization Sp³ Bond angle 109.5° Total Valence electron for CH4 8 The formal charge of CH4 0
How to draw the lewis structure of CH4 (Methane)?
CH4 lewis’s structure is very simple and easy to draw, it is made up of one carbon atom that takes the central position and four hydrogens that spread around the central atom. There are no lone pair electrons present in the lewis dot structure of CH4.
Let’s see how to draw the lewis structure by following some simple steps:
Basic steps for drawing the Lewis spot structure
1. Include all out valence electron
In the initial step, we need to observe the number of valence electrons is there in CH4, so we can disseminate them around focal and terminal molecules determined to finish their octet shell.
-
You have two methods for discovering the valence electron for a specific iota, either by taking a gander at their intermittent gathering or by composing their electronic design. We will involve the technique for the intermittent gathering for tracking down the valence electron.
-
The carbon iota has a place with Gathering 4A or 14A in the intermittent table, henceforth, it has a 4 valence electron in its furthest shell while the hydrogen molecule has a place with Gathering 1A, subsequently, it has just 1 valence electron in its peripheral shell.
⇒ All out valence electron in Carbon = 4
⇒ All out valence electron in Hydrogen = 1
∴ All out valence electron accessible for drawing the CH4 lewis structure = 4 + 1*4 = 8 valence electrons [∴CH4 has four hydrogen molecules and one carbon atom]
2. Find the least electronegative atom and placed it at center
At whatever point hydrogen is available in any particle then it doesn’t make any difference which iota is less or more electronegative, hydrogen consistently goes outside in a lewis graph and it needs just two electrons to finish its external shell.
Thus, place all Hydrogen molecules outside in the lewis graph and the Carbon particle at the focal position.
3. Associate each external particle to the focal molecule with a solitary bond
In this progression, we will interface each external iota (which is hydrogen in the CH4 particle) to the focal atom(carbon) with the assistance of a solitary bond.
-
Presently see this construction and count the number of electrons we utilized till now and the number of are left.
-
As four single bonds are utilized in the above structure that contains 8 electrons(1 single bond implies 2 electrons) and we have an aggregate of 8 valence electrons are accessible for drawing the CH4 lewis structure.
(8 – 8) = 0 valence electrons
Thus, we involved all accessible valence electrons in the above structure, presently including the electrons in the valence or external shell of every iota to know whether they finished their octet or not.
-
“The octet rule alludes to the propensity of molecules to like to have eight electrons in the valence shell”.
-
The particle which has less or over 8 electrons in the valence shell, are named Uncommon to the octet rule.
-
The carbon iota needs 8 electrons in its valence shell to finish the octet, on the off chance that you see the above structure, the carbon focal molecule is connected with four single bonds, which implies, it has currently 8 electrons in its external shell, subsequently, the carbon particle finished its octet easily.
Summary
The hydrogen iota just requires two valence electrons for finishing the octet as it is uncommon to the octet. In this way, in the above structure, every hydrogen molecule is appended to the single bond, which implies, they as of now have two electrons in their external shell, henceforth, hydrogen particles likewise finished their octet rule serenely.
CH4 lewis structure
As you find in this CH4 lewis structure, carbon focal particle and hydrogen iota finished their octet, and all that looks fine, however, for the fulfillment, we ought to likewise decide the conventional charge in the above design to know whether or not it is steady.
-
- Really take a look at the security with the assistance of a proper charge idea
-
A proper charge is the charge appointed to an iota in a particle, expecting that electrons in all compound bonds are shared similarly between molecules.
-
The design with the conventional charge near nothing or zero is an awesome and stable lewis structure.
-
To compute the conventional charge in the CH4 lewis structure. Utilize the equation given beneath
-
We should begin with the focal iota which is carbon in the CH4 atom.
For carbon iota:
⇒ Valence electrons of carbon = 4
⇒ Solitary pair electrons on carbon = 0
⇒ Holding electrons of carbon(4 single bonds) = 8
∴ (4 – 0 – 8/2) = 0 conventional charge on the carbon focal particle.
Every hydrogen iota in the CH4 lewis structure has a similar number of fortified pair electrons, thus, simply count formal charge for only one hydrogen particle, rest all will follow it.
For hydrogen molecule
⇒ Valence electrons of hydrogen = 1
⇒ Solitary pair electrons on hydrogen = 0
⇒ Holding electrons around hydrogen (1 single bond) = 2
∴ (1 – 0 – 2/2) = o formal charge on every hydrogen iota.
Henceforth, every iota in CH4 gets a conventional charge equivalent to nothing.
In this way, the above lewis construction of CH4 (Methane) is the most steady, fing, and dependable.
What are the electron and atomic calculation of CH4 (Methane)?
The sub-atomic calculation of CH4 is tetrahedral as the carbon focal iota has no solitary pair and is appended to the four hydrogen molecules with the assistance of a solitary covalent bond. In this way, there are four locales of electron thickness around the carbon focal iota".
-
The electron pair around the carbon focal iota will repulse one another and attempt to go a long way from one another, they will take the position where aversion becomes least between them.
-
As indicated by the VSEPR hypothesis, “in a large portion of the cases, the focal particle with four areas of thickness take on a tetrahedral structure since aversion is least in electron sets at this position.”
-
In the above figure, the red lines layout the tetrahedron, and the dark line shows the reinforced pair or electron pair shaped among carbon and hydrogen. “The carbon iota is situated in the focal point of the tetrahedron, while the four hydrogens molecules are situated on the vertices.”
-
In this way, there are four holding sets framed in CH4 particle, thus, as per the VSEPR hypothesis, they will repulse one another, therefore, all corners atoms(hydrogens) spread out however much they can and has the spot where the shock is least and security is greatly improved.
-
Subsequently, the last atomic math of CH4 seems like a standard tetrahedron with a bond point ∠H−C−H =109.5°.
-
Assuming you can’t envision the sub-atomic calculation of CH4, then, at that point, hypothetically we can utilize an AXN technique and VSEPR outline to decide its shape.
-
AXN is a straightforward recipe that addresses the quantity of the fortified particle and solitary pair on the focal iota to anticipate the state of the atom utilizing the VSEPR outline.
AXN notation for CH4 molecule:
A means the focal iota, in this way, in the CH4 particle, carbon is the focal molecule. A = Carbon
-
X means the fortified iotas to the focal particle, as we probably are aware, the carbon focal molecule is reinforced with four hydrogen iotas. Hence, X = 4
-
N means the solitary pair on the focal particle, according to CH4 lewis structure, carbon focal iota doesn’t contain any solitary pair. Henceforth, N = 0
-
In this way, the AXN documentation for the CH4 particle becomes AX4N0 or AX4.
-
According to the VSEPR diagram, assuming a particle’s focal iota is joined with four fortified iotas and has contained no solitary pair on the focal iota then the sub-atomic math of that particle is tetrahedral in nature, and its electron calculation is likewise tetrahedral.
-
Subsequently, the sub-atomic calculation for CH4 is tetrahedral and its electron math is likewise tetrahedral.
-
CH4 sub-atomic calculation/shape
Hybridization of CH4
How about we track down the hybridization of CH4 through the steric number of its focal particle.
-
“Steric number is the expansion of an absolute number of fortified particles around a focal molecule and the solitary pair present on it.”
-
Steric number of CH4 = (Number of fortified particles joined to carbon iota + Solitary pair on carbon molecule)
-
According to the lewis construction of CH4, the focal Carbon particle is fortified with four hydrogen iotas and it doesn’t have any solitary pair.
Seric number of CH4 = (4 + 0) = **4
Steric number Hybridization 1 S 2 Sp 3 Sp² 4 Sp³ 5 Sp³d 6 Sp³d²
In this way, for a steric number of four, we get the Sp3 hybridization on a carbon particle in the CH4 atom.
The recently created crossover orbitals in the CH4 atom have 25% conduct of the s orbital and 75% conduct of the p orbital.
The bond point of CH4
As we probably are aware the sub-atomic math of CH4 is customary tetrahedral with no contortion, henceforth, as indicated by the VSEPR hypothesis, for an ordinary tetrahedral structure, the reinforced iotas around the focal particle will spread at a point of approx 109.5° to limit the shock and achieves security.
-
Thus, the bond point of ∠H−C−H in CH4 is 109.5°.
-
Methane extremity: is CH4 polar or nonpolar
-
All things considered, we realize the polar atom has some dipole second as a result of inconsistent conveyance of charges while the non-polar particle has an equivalent dispersion of charges that cause zero dipoles second since they counteract each other because of the even state of the particle.
-
Is Methane (CH4) polar or non-polar? CH4 is a non-polar particle since it contains four bonds(C-H) that are organized evenly in tetrahedral mathematical shapes. Because of this, dipole second created on each side along C-H will offset each other making a generally nonpolar atom.
-
We should comprehend whether CH4 is polar or non-polar exhaustively.
Three factors that show the extremity of CH4
Electronegativity:
It straightforwardly impacts the extremity idea of any iota or particle in light of the fact that the extremity is straightforwardly corresponding to the distinction of electronegativity made by iotas or atoms. Electronegativity implies the inclination of a molecule to drawing in electrons towards itself.
-
On the off chance that the electronegativity contrast between the particles is high then the extremity will likewise be higher. Presently, check out the electronegativity of carbon and hydrogen.
-
As carbon electronegativity is around 2.6 and for hydrogen, it is around 2.2. Hence, carbon has a higher propensity to draw in an electron to itself than hydrogen.
-
Likewise, the electronegativity contrast between carbon and hydrogen is under 0.5, and as per the Pauling scale assuming the electronegativity distinction between iotas is lower than 0.5 then the connection between those particles acts as nonpolar.
-
Note: It doesn’t require assuming that some bond is polar then the entire atom can likewise be polar. On account of CO2, the C-O bond is polar in nature because of the distinction in electronegativity between them is more than 0.5. However, the entire atom of CO2 is non-polar in nature because of its even shape.
-
Accordingly, in the event that we consider the C-H securities polar, then, at that point, all dipoles created along these bonds will counterbalance each other in light of the balanced tetrahedral math of CH4 bringing about a generally nonpolar atom.
2. Dipole second
Dipole second guarantees the strength of extremity among carbon and hydrogen particles. As more prominent the dipole snapshot of the particle, the more is the polar idea of that atom. The electronegativity contrast between the atoms(Carbon and hydrogen) prompted positive and negative charges.
-
As carbon is more electronegative than hydrogen, henceforth, some bad charge is prompted on the carbon molecule and a halfway certain charge is actuated on the hydrogen iotas. In this way, these charges make four dipole minutes alongside C–H bond. How about we see the figure given beneath.
-
As dipole second incited toward the path from hydrogen to carbon since carbon is more electronegative than hydrogen, thus, it draws in electrons towards itself.
-
In any case, dipole minutes created along these bonds can without much of a stretch be counteracted of one another on the grounds that the CH4 has a customary construction of tetrahedral with no solitary pair on the focal molecule.
-
In numerical terms, we can communicate dipole second as D = Q×R
-
Dipole second equation = charge on the molecules * the distance between them.
3. Mathematical or sub-atomic shape:
The mathematical construction of any atom has extraordinary effects on the extremity nature. As the CH4 sub-atomic math is tetrahedral that has four nonpolar covalent bonds (C-H) however all they are the other way.
-
Additionally, a focal particle of CH4 doesn’t contain any solitary pair which makes its atom shape profoundly symmetric.
-
Thus, the C-H bonds are exceptionally symmetric and inverse in bearing which can without much of a stretch be counterbalanced each other making this particle become non-polar in nature.
Why is the molecular geometry of CH4 is same as its electron geometry?
The sub-atomic math of CH4 is tetrahedral and its electron calculation is additionally tetrahedral in light of the fact that according to VSEPR hypothesis, sub-atomic shape considers just bond sets or molecules while electron calculation considers reinforced particles just as solitary sets present on the focal iota.
1. As per the lewis construction of CH4, the focal atom(carbon) doesn’t contain any solitary pair on it.
2. Subsequently, just reinforced iotas are utilized to decide the calculation of CH4.
3. Subsequently, Sub-atomic math of CH4 = Electron calculation of CH4 .
What number of solitary matches and bond sets are available around the carbon focal molecule in the CH4 lewis structure?
As per the lewis speck design of CH4, the Carbon focal particle doesn’t contain any solitary pair yet is connected to the four hydrogen molecules with the assistance of four fortified sets
Important Key Factors
The complete valence electron accessible for drawing the Methane (CH4) lewis structure is 8.
-
The steric number of the focal particles in methane is 4 that guarantees that it has a Sp3 hybridization.
-
CH4 is a nonpolar particle because of its even calculation that causes uniform charge appropriation all around the iota prompts a zero net dipole second and makes this atom non-polar in nature.
-
The atomic math or shape for CH4 is the tetrahedral with bond point ∠H−C−H =109.5°.
-
The electron math for CH4 is likewise tetrahedral as it focal has 4 locales of electron thickness with no solitary pair on it.
-
Lewis spot design of CH4 contains just 4 fortified pairs(8 shared electrons) and doesn’t contain any solitary pair electrons in the particle.
Summary
The VSEPR hypothesis says that electron sets, likewise a bunch of like charges, will repulse each other with the end goal that the state of the atom will change so the valence electron-sets stay as far separated from one another as could really be expected.
Sub-atomic Shapes
The leaves repulse each other since both hold positive, similar charges.
HOW DOES AN ELECTROSCOPE Function?
An electroscope is a gadget used to concentrate on charge. At the point when an emphatically charged item (the pole) approaches the upper post, electrons stream to the highest point of the container leaving the two gold leaves positively charged.
Focal Particle with No Solitary Sets
To handily comprehend the sorts of atoms conceivable, we will utilize a basic framework to distinguish the pieces of any particle.
A = focal particle in an atom
B = molecules encompassing the focal iota
1. Addendums later the B will indicate the number of B particles that are clung to the focal A molecule.
2. For instance, Stomach muscle 4 is a particle with a focal iota encompassed by four covalently fortified molecules. Once more, it doesn’t make any difference assuming those bonds are single, twofold, or triple bonds.
AB2: Beryllium hydride (BeH2)
Beryllium hydride comprises focal beryllium molecule with two single bonds to hydrogen particles. Review that it disregards the octet rule.
H-Be-H
As indicated by the prerequisite that electron sets amplify their separation from each other, the two holding sets in the BiH 2 particles will orchestrate themselves on straightforwardly inverse sides of the focal Be iota. The subsequent math is a straight atom, displayed In a “ball and stick” model.
The bond point from H-Be-H is 180° as a result of its straight math.
-
Carbon dioxide is one more illustration of an atom that falls under the Abdominal muscle 2 class. Its Lewis structure comprises of twofold connections between the focal carbon and the oxygen molecules.
-
The repugnance between the two gatherings of four electrons (two sets) is the same as the aversion of the two gatherings of two electrons (one set) in the BeH 2 particle. Carbon dioxide is likewise straight.
AB3: Boron Trifluoride (BF3)
Boron trifluoride comprises of a focal boron iota with three single bonds to fluorine molecules . The boron iota additionally has an inadequate octet.
The math of the BF 3 atom is called three-sided planar… The fluorine particles are situated at the vertices of a symmetrical triangle. The F-B-F point is 120° and each of the four molecules lie in a similar plane.
AB4: Methane (CH4)
Methane is a natural compound that is the essential part of flammable gas. Its construction comprises of a focal carbon iota with four single bonds to hydrogen particles. To augment their separation from each other, the four gatherings of holding electrons don’t lie in a similar plane.
-
All things being equal, every one of the hydrogen molecules lies at the edges of a mathematical shape called a tetrahedron. The carbon molecule is at the focal point of the tetrahedron. Each face of a tetrahedron is a symmetrical triangle.
-
The atomic math of the methane particle is tetrahedral. The H-C-H bond points are 109.5°, which is bigger than the 90° that they would be assuming the atom was planar. When drawing a primary equation for a particle, for example, methane, it is beneficial to have the option to show the three-layered person of its shape.
-
The primary recipe beneath is known as a point of view drawing. The dabbed line bond is to be pictured as subsiding into the page, while the strong triangle bond is to be imagined as emerging from the page.
Central Atom with One or More Lone Pairs
The sub-atomic calculations of particles change when the focal iota has at least one solitary sets of electrons. The complete number of electron sets, both holding sets and solitary sets, prompts what is known as the electron space math.
-
At the point when at least one of the holding sets of electrons is supplanted with a solitary pair, the sub-atomic calculation (real state) of the particle is adjusted.
-
With regards to the An and B images set up in the past area, we will utilize E to address a solitary pair on the focal particle (A). An addendum will be utilized when there is more than one solitary pair. Solitary sets on the encompassing particles (B) don’t influence the calculation.
AB3E: Smelling salts, NH3
The smelling salts particle contains three single bonds and one solitary pair on the focal nitrogen iota .
-
The area calculation for a particle with four electron sets is tetrahedral, as was seen with CH 4 . In the alkali particle, one of the electron sets is a solitary pair rather than a holding pair. The sub-atomic math of NH 3 is called three-sided pyramidal.
-
Review that the bond point in the tetrahedral CH 4 particle is 109.5°. Once more, the substitution of one of the fortified electron sets with a solitary pair packs the point marginally. The H-N-H point is roughly 107°.
AB2E2: Water, H2O
A water atom comprises of two holding sets and two solitary sets .Concerning methane and smelling salts, the area calculation for a particle with four electron sets is tetrahedral. In the water particle, two of the electron sets are solitary matches rather than holding sets.
The sub-atomic calculation of the water particle is bowed. The H-O-H bond point is 104.5°, which is more modest than the bond point in NH3
AB4E: Sulfur Tetrafluoride, SF4
The Lewis structure for SF 4 contains four single bonds and a solitary pair on the sulfur molecule. The sulfur molecule has five electron bunches around it, which relates to the three-sided bipyramidal space math, as in PCl 5 (see Figure 13).
Review that the three-sided bipyramidal calculation has three tropical molecules and two pivotal iotas joined to the focal particle. In view of the more prominent aversion of a solitary pair, it is one of the central iotas that are supplanted by a solitary pair. The calculation of the particle is known as a contorted tetrahedron or teeter-totter.
Here, I described a Ball and stick model for SF 4 .
Total Number of Electron Pairs Number of Bonding Pairs Number of Lone Pairs Electron Domain Geometry Molecular Geometry Examples 3 2 1 trigonal planar bent O3 4 3 1 tetrahedral trigonal pyramidal NH3 4 2 2 tetrahedral bent H2O 5 4 1 trigonal bipyramidal distorted tetrahedron (seesaw) SF4
How Would We Know Methane (CH4) Is Tetrahedral?
What Do The Valence Electrons Of Carbon Enlighten Us Concerning The Holding In CH4?
Assuming the orbital design of carbon is 2s22p2 , then, at that point, how might we utilize this data to sort out what the game plan of the orbitals are in a straightforward natural atom like methane (CH4)?
-
It just so happens, methane is tetrahedral, with 4 equivalent bond points of 109.5° and 4 equivalent bond lengths, and no dipole second.
-
This raises two inquiries. To start with, how do we have any idea about that CH4 is tetrahedral? Furthermore besides, how would we accommodate this electronic arrangement (2s22p2 ) with the way that we have four equivalent C–H bonds?
1. The Electronic Design Of The Valence Electrons Of Carbon Is 2s22p2
In our survey of nuclear orbitals, we saw that the orbital arrangement of the valence electrons of carbon is 2s22p2 as displayed beneath:
1. Since the 2s orbital is lower in energy than 2p, it’s filled first. That implies that there are two electrons during the 2s orbital, and a solitary electron in two of the three 2p orbitals. There’s likewise a void 2p orbital.
2. [Furthermore, there are two electrons in the “inward shell” 1s orbital, which are not accessible for bonding].
2. Would we be able to Utilize This Data To Sort Out The Construction Of Methane (CH4)? (Spoiler: No)
No issues up until now. This is fine assuming that we’re simply discussing segregated carbon particles.
1. In any case, to be really valuable, we should have the option to relate the orbitals of carbon to the construction and holding of real natural mixtures.
2. The least difficult natural compound is methane, CH4. So we should bring four hydrogen iotas into the image and attempt to apply what we’ve figured out how to think of certain theories about the holding in this particle.
The 3 p-orbitals in carbon are all at 90 degrees to one another, along the x, y, and z tomahawks.
Shouldn’t we expect that the construction of methane would have three C-H bonds for every one of the p orbitals (at 90 degrees to one another) and afterward the fourth C-H bond joined to the 2s orbital? Since electron sets repulse, possibly we should put that C-H bond the greatest separation away from the other C-H bonds; this would give a H–C–H bond point of 135°.
Following this rationale would give a construction like this:
Incidentally, it very well may be shown that this proposition is off-base.
Why?
Dipole second.
Review that every C–H bond has a little dipole because of the distinction in electronegativity between C (2.5) and H (2.2). We anticipate that C should be somewhat negative and H to be to some degree positive.
-
On the off chance that the above structure precisely portrayed the construction of methane, we’d anticipate that methane should have 3 longer C–H clings (to the 2p orbitals) and one more limited C–H attach (to the 2s orbital, which is nearer to the core)
-
Moreover, we’d expect 3 H–C–H bond points of 90° and one H–C–H bond point of 135°.
-
At the point when the vector amounts of the C–H dipoles are accumulated in this construction, they would not all counteract.
-
We would in this way hope to notice a little, however quantifiable dipole second for CH4. [note 1]
-
Nonetheless, the deliberate dipole snapshot of CH4 is zero. Hence this can’t be the right construction.
-
This lets us know that all the bond lengths and bond points in methane are indistinguishable.
3. Possibly Methane (CH4) Is Square Planar?
Okay, you say. Assuming all C-H bonds are of equivalent lengths and points, for what reason can’t CH4 have the design beneath, where all the bond points are 90° and CH4 is level, in the plane of the page. (We refer to this construction as “square planar”).
-
This was truth be told the larger part assessment for the course of action of bonds around carbon until around 1880. Incredibly splendid scientists, for example, Berzelius went to their graves having no real excuse to question that methane was everything except level.
-
Nonetheless, we presently realize that this generally will be off-base. Why?
4. Discrediting The Square Planar degree Of CH4 (1874)
Assuming methane is altered so the focal carbon is appended to four unique gatherings, the atom can exist as 2 distinct isomers that are non-superimposable perfect representations (this is classified “optical isomerism” and shrouded later in the course).
-
This is conceivable assuming the course of action of 4 gatherings around the focal carbon is tetrahedral, yet not on the off chance that the atom is square planar.
-
For instance, the methane subordinate bromochlorofluoromethane has four unique gatherings around carbon and can be isolated into two distinct isomers which pivot plane-energized degree in various ways. [As we’ll see later, these isomers are classified “enantiomers”]
This perception precludes the square planar design. Assuming carbon was square planar, the particle would be level, and be superimposable on its own identical representation, and just a single isomer would be conceivable.
Jacobus Henricus van’t Hoff , an individual at the veterinary school in Utrecht, was among quick to address the chance of three-layered carbon. In his “La Chimie dans L’Espace” (1874) he noticed that the course of action of particles in space has significant commonsense outcomes.
Point that had been totally forgotten to that point. van’t Hoff showed that a tetrahedral plan of four unique gatherings around a carbon molecule (which he called an “deviated carbon”) would bring about two distinct isomers, and besides, this would clarify why tartaric corrosive (with two lopsided carbon particles) existed in three structures (+, – , and meso).
Van’t Hoff’s work – which ought to be noted was simply hypothetical – was not generally welcomed in certain circles.
5. Tetrahedral Carbons: Not A Well known Thought In 1874
As far as concerns him, van’t Hoff traveled to degree on his Pegasus to get the primary Nobel Prize in Science in 1901. [Note 2]
Indisputable verification for the tetrahedral game plan of bonds around the carbon particle came in 1913 not really set in stone the construction of jewel utilizing X-beam crystallography and viewed it as a tetrahedral organization of carbon molecules with C-C-C bond points of 109.5°.
6. So What Orbitals ARE Involved?
We currently justify the tetrahedral course of action of degree around methane as being because of the shock of the holding sets of electrons with one another (a.k.a. VSEPR hypothesis).
-
This doesn’t assist us with comprehension the orbitals associated with holding, in any case.
-
Assuming we acknowledge that the plan of hydrogens around methane is tetrahedral, then, at that point, how would we portray the holding orbitals of methane, considering what we are familiar the math of s and p orbitals?
-
All things considered, the 2p orbitals are all at 90 degrees to one another, yet the bond points in methane are 109.5°.
-
Moreover, how would we account that every one of the 4 bonds in methane are of indistinguishable lengths? What befell the 2s orbital, for instance?
-
Are the electrons in the C-H bonds viewed as in p orbitals or s orbitals? Or on the other hand something different?
-
For reasons unknown, the customary treatment is to manage the bonds around carbon as being in mixture orbitals.
SUMMARY
Electron sets repulse one another and impact bond points and sub-atomic shape. The presence of solitary pair electrons impacts the three-layered state of the particle. The particle around which different molecules are organized.
Notes
1. Note that mono-deuterated methane (CH3D, where D is deuterium, the weighty isotope of hydrogen) has a little dipole second that has been estimated. [ref]
2. Note 2: it ought to be noticed that van’t Hoff’s Nobel Prize was for his commitments to actual science, not natural stereochemistry.
3. I’m obligated to this page covering van’t Hoff’s “The Plan of Particles In Space” for recorded viewpoint. Certainly worth perusing in full.
4. From a similar source: van’t Hoff’s tetrahedral models [from the Leiden history of science historical center; source]
5. From a similar creator, some more degree point of view on the Kolbe/van’t Hoff spat:
6. Clearly Kolbe was senseless to be so excessive and resentful. He was likewise childish, and he speculated wrong. We can undoubtedly see the value in that in the court of history he got what was coming to him.
7. The test is appropriately to regard the irreplaceable commitments the demeanor he was advocating had made to the improvement of science. It was by adhering near cautious test perceptions that science had gotten where it was (and is). Kolbe was attempting to keep science on a useful, mentally legitimate way.
The State of Atoms
The three layered shape or setup of an atom is a significant trademark. This shape is reliant upon the favored spatial direction of covalent bonds to particles having at least two holding accomplices. Three layered designs are best seen with the guide of models. To address such designs on a two-layered surface (paper, chalkboard or screen), we regularly utilize point of view drawings in which the heading of a bond is determined by the line interfacing the reinforced particles.
-
As a rule the focal point of arrangement is a carbon particle so the lines indicating bond headings will start there. As characterized in the outline on the right, a straightforward straight line addresses a bond lying around in the surface plane.
-
The two bonds to substituents An in the design on the left are of this sort. A wedge formed bond is coordinated before this plane (thick end toward the watcher), as shown by the cling to substituent B; and an incubated bond is coordinated toward the rear of the plane (away from the watcher), as shown by the cling to substituent D.
-
A few messages and different sources might involve a ran bond in a similar way as we have characterized the brought forth bond, however this can be confounding in light of the fact that the ran bond is frequently used to address an incomplete bond (for example a covalent bond that is to some extent framed or to some degree broken).
-
The accompanying models utilize this documentation, and furthermore delineate the significance of including non-holding valence shell electron sets (shaded blue) when survey such setups .
Holding setups are promptly anticipated by valence-shell electron-pair shock hypothesis, usually alluded to as VSEPR in most basic science texts.
This basic model depends on the way that electrons repulse one another, and that it is sensible to expect that the bonds and non-holding valence electron sets related with a given particle will like to be as far separated as could really be expected. The holding designs of carbon are not difficult to recollect, since there are just three classes.
-
In In the three models displayed over, the focal molecule (carbon) doesn’t have any non-holding valence electrons; therefore the arrangement might be assessed from the quantity of holding accomplices alone. For particles of water and smelling salts, be that as it may, the non-holding electrons should be remembered for the estimation. For each situation there are four locales of electron thickness related with the valence shell so that a tetrahedral bond point is normal.
-
The deliberate security points of these mixtures (H2O 104.5º and NH3 107.3º) show that they are nearer to being tetrahedral than three-sided or straight. Obviously, it is the setup of iotas (not electrons) that characterizes the state of an atom, and in this sense smelling salts is supposed to be pyramidal (not tetrahedral).
-
The compound boron trifluoride, BF3, doesn’t have non-holding valence electrons and the setup of its particles is three-sided. Decent medicines of VSEPR hypothesis have been given by Oxford and Purdue . Click on the college name to visit their site.
-
The most effective way to concentrate on the three-layered states of atoms is by utilizing sub-atomic models. Numerous sorts of model units are accessible to understudies and expert scientists.
-
A portion of the helpful highlights of actual models can be approximated by the model survey applet Jmol. This strong perception instrument permits the client to move an atomic stucture in any capacity wanted.
-
Particle distances and points not really set in stone. To quantify a distance, double tap on two molecules. To gauge a bond point, do a double tap, single-tick, double tap on three particles. To gauge a twist point, do a double tap, single-tick, single-tick, double tap on four particles.
-
A spring up menu of orders might be gotten to by the right button on a PC or a control-click on a Macintosh while the cursor is inside the presentation outline.
-
You might look at a few Jmol models of mixtures examined above by .
-
One manner by which the states of particles manifest themselves tentatively is through atomic dipole minutes. A particle which has at least one polar covalent bonds might have a dipole second because of the collected bond dipoles.
-
On account of water, we realize that the O-H covalent bond is polar, because of the various electronegativities of hydrogen and oxygen. Since there are two O-H bonds in water, their bond dipoles will connect and may bring about a sub-atomic dipole which can be estimated.
-
The accompanying graph shows four potential directions of the O-H bonds.
-
The bond dipoles are shaded red and the subsequent atomic dipole is hued blue. In the straight setup (bond point 180º) the bond dipoles drop, and the atomic dipole is zero. For other bond points (120 to 90º) the atomic dipole would change in size, being biggest for the 90º arrangement.
-
Along these lines the arrangements of methane (CH4) and carbon dioxide (CO2) might be found from their zero sub-atomic dipole minutes. Since the bond dipoles have dropped, the designs of these atoms should be tetrahedral (or square-planar) and straight.
-
The instance of methane gives knowledge to different contentions that have been utilized to affirm its tetrahedral setup. For motivations behind conversation we will consider three different setups for CH4, square-planar, square-pyramidal and three-sided pyramidal.
-
Models of these conceivable outcomes might be inspected by .
-
Replacement of one hydrogen by a chlorine particle gives a CH3Cl compound. Since the tetrahedral, square-planar and square-pyramidal setups have basically identical hydrogen particles, they would each give a solitary replacement item.
-
Nonetheless, in the three-sided pyramidal arrangement one hydrogen (the peak) is fundamentally unique in relation to the next three (the pyramid base). Replacement for this situation should give two distinct CH3Cl compounds assuming every one of the hydrogens respond.
-
On account of disubstitution, the tetrahedral setup of methane would prompt a solitary CH2Cl2 item, yet different arrangements would give two distinct CH2Cl2 compounds. These replacement prospects are displayed in the above embed.
Isomers
Underlying Equations
It is important to draw underlying equations for natural mixtures on the grounds that much of the time an atomic recipe doesn’t extraordinarily address a solitary compound. Various mixtures having a similar sub-atomic equation are called isomers, and the pervasiveness of natural isomers mirrors the unprecedented flexibility of carbon in framing solid bonds to itself and to different components.
-
At the point when the gathering of iotas that make up the particles of various isomers are fortified together in generally various ways, we allude to such mixtures as established isomers.
-
There are seven protected isomers of C4H10O, and underlying recipes for these are attracted the accompanying table. These equations address all known and conceivable C4H10O mixtures, and show a typical primary component.
-
There are no twofold or triple bonds and no rings in any of these designs… Note that every one of the carbon iotas is attached to four different particles, and is soaked with holding accomplices.
-
Disentanglement of primary recipes might be accomplished with no deficiency of the data they pass on. In consolidated primary recipes the bonds to every carbon are excluded, however each unmistakable underlying unit (bunch) is composed with addendum numbers assigning different substituents, including the hydrogens. Shorthand (line) recipes discard the images for carbon and hydrogen totally.
-
Every straight line section addresses a bond, the closures and convergences of the lines are carbon particles, and the right number of hydrogens is determined from the tetravalency of carbon. Non-holding valence shell electrons are overlooked in these equations.
-
Fostering the capacity to picture a three-layered construction from two-layered recipes requires practice, and much of the time the guide of atomic models. As noted before, numerous sorts of model units are accessible to understudies and expert physicists, and the starting understudy is urged to get one.
Recognizing Carbon Molecules
While examining underlying recipes, it is regularly valuable to recognize various gatherings of carbon molecules by their primary qualities. An essential carbon (1º) is one that is clung to something like another carbon iota.
-
An auxiliary carbon (2º) is clung to two other carbon molecules, and tertiary (3º) and quaternary (4º) carbon particles are reinforced individually to three and four different carbons. The three C5H12 isomers displayed beneath represent these terms.
-
Underlying contrasts might happen inside these four gatherings, contingent upon the sub-atomic constitution. In the equation on the right each of the four 1º-carbons are fundamentally same (recall the tetrahedral design of tetravalent carbon); but the focal recipe has two identical 1º-carbons (clung to the 3º carbon on the left end) and a solitary, primarily unique 1º-carbon (attached to the 2º-carbon) at the right end.
-
Likewise, the furthest left equation has two basically comparable 2º-carbons (close to the closures of the chain), and a fundamentally unique 2º-carbon in the chain.
-
A thought of sub-atomic evenness assists with recognizing primarily comparable from nonequivalent molecules and gatherings. The capacity to recognize underlying contrasts of this sort is a fundamental piece of dominating natural science. It will accompany practice and experience.
Examination of Sub-atomic Equations
Albeit primary recipes are fundamental for the novel portrayal of natural mixtures, it is intriguing and enlightening to assess the data that might be gotten from an atomic equation alone. Three helpful principles might be recorded:
-
The quantity of hydrogen particles that can be attached to a given number of carbon molecules is restricted by the valence of carbon. For mixtures of carbon and hydrogen (hydrocarbons) the greatest number of hydrogen iotas that can be attached to n carbons is 2n + 2 (n is a number).
-
On account of methane, CH4, n=1 and 2n + 2 = 4. The beginning of this recipe is clear by considering a hydrocarbon comprised of a chain of carbon molecules. Here the center carbons will each have two hydrogens and the two end carbons have three hydrogens each.
-
Hence, a six-carbon chain (n = 6) might be composed H-(CH2)6-H, and the complete hydrogen count is (2 x 6) + 2 = 14. The presence of oxygen (valence = 2) doesn’t change this relationship, so the recently depicted C4H10O isomers adhere to the guideline, n=4 and 2n + 2 = 10. Halogen particles (valence = 1) ought to be counted comparable to hydrogen, as shown by C3H5Cl3, n = 3 and 2n + 2 = 8 = (5 + 3). Assuming nitrogen is available, every nitrogen iota (valence = 3) expands the most extreme number of hydrogens by one.
Some Plausible
Molecular Formulas C7H16O3, C9H18, C15H28O3, C6H16N2
Some Impossible
Molecular Formulas C8H20O6, C23H50, C5H10Cl4, C4H12NO
For stable organic compounds the total number of odd-valenced atoms is even. Thus, when even-valenced atoms such as carbon and oxygen are bonded together in any number and in any manner, the number of remaining unoccupied bonding sites must be even.
If these sites are occupied by univalent atoms such as H, F, Cl, etc. their total number will necessarily be even. Nitrogen is also an odd-valenced atom (3), and if it occupies a bonding site on carbon it adds two additional bonding sites, thus maintaining the even/odd parity.
Some Plausible
Molecular Formulas C4H4Cl2, C5H9OBr, C5H11NO2, C12H18N2FCl
Some Impossible
Molecular Formulas C5H9O2, C4H5ClBr, C6H11N2O, C10H18NCl2
The number of hydrogen atoms in stable compounds of carbon, hydrogen & oxygen reflects the number of double bonds and rings in their structural formulas. Consider a hydrocarbon with a molecular structure consisting of a simple chain of four carbon atoms, CH3CH2CH2CH3. The molecular formula is C4H10 (the maximum number of bonded hydrogens by the 2n + 2 rule).
1. If the four carbon atoms form a ring, two hydrogens must be lost. Similarly, the introduction of a double bond entails the loss of two hydrogens, and a triple bond the loss of four hydrogens.
2. From the above discussion and examples it should be clear that the molecular formula of a hydrocarbon (CnHm) provides information about the number of rings and/or double bonds that must be present in its structural formula. By rule #2 m must be an even number, so if m < (2n + 2) the difference is also an even number that reflects any rings and double bonds. A triple bond is counted as two double bonds.
The presence of one or more nitrogen atoms or halogen substituents requires a modified analysis. The above formula may be extended to such compounds by a few simple principles:
-
The presence of oxygen does not alter the relationship.
-
All halogens present in the molecular formula must be replaced by hydrogen.
-
Each nitrogen in the formula must be replaced by a CH moiety.
Resonance
Reverberation
Kekulé underlying recipes are fundamental instruments for understanding natural science. In any case, the designs of certain mixtures and particles can’t be addressed by a solitary recipe. For instance, sulfur dioxide (SO2) and nitric corrosive (HNO3) may each be depicted by two comparable recipes (conditions 1 and 2). For lucidity the two uncertain bonds to oxygen are given various tones in these equations.
-
The above models address one limit in the use of reverberation. Here, two fundamentally and vivaciously comparable electronic constructions for a steady compound can be composed, yet no single design gives a precise or even a satisfactory portrayal of the genuine atom.
-
In cases, for example, these, the electron delocalization portrayed by reverberation improves the steadiness of the particles, and mixtures or particles made out of such atoms regularly show extraordinary soundness.
-
The electronic constructions of most covalent mixtures don’t experience the insufficiency noted previously. In this manner, totally palatable Kekulé recipes might be drawn for water (H2O), methane (CH4) and acetylene C2H2). In any case, the standards of reverberation are exceptionally helpful in justifying the synthetic conduct of many such mixtures.
-
For instance, the carbonyl gathering of formaldehyde (the carbon-oxygen twofold bond) responds promptly to give expansion items. The course of these responses can be clarified by a little commitment of a dipolar reverberation giver, as displayed in condition 3.
-
Here, the main patron (on the left) is obviously the best portrayal of this sub-atomic unit, since there is no charge division and both the carbon and oxygen molecules have accomplished valence shell neon-like arrangements by covalent electron sharing. Assuming that the twofold bond is broken heterolytically, formal charge sets result, as displayed in the other two designs.
-
The favored charge dispersion will have the positive charge on the less electronegative particle (carbon) and the negative charge on the more electronegative molecule (oxygen). Accordingly the center recipe addresses a more sensible and stable design than the one on the right. The utilization of reverberation to this case requires a weighted averaging of these standard designs.
-
The twofold fortified design is viewed as the significant benefactor, the center construction a minor donor and the right hand structure a non-giver. Since the center, charge-isolated supporter has an electron insufficient carbon molecule, this clarifies the inclination of electron contributors (nucleophiles) to bond at this site.
-
The standards of the reverberation strategy may now be summed up.
-
For a given compound, a bunch of Lewis/Kekulé structures are composed, keeping the general places of all the part iotas the equivalent. These are the accepted structures to be thought of, and all should have similar number of matched and unpaired electrons.
-
The accompanying variables are significant in assessing the commitment every one of these sanctioned designs makes to the real atom.
-
The quantity of covalent bonds in a construction. (The more noteworthy the holding, the more significant and stable the contributing design.)
-
Formal charge partition. (Different factors to the side, charge partition diminishes the dependability and significance of the contributing construction.) of charge bearing atoms and charge density.
-
High charge thickness is weakening. Positive charge is best obliged on iotas of low electronegativity, and negative charge on high electronegativ molecules.es
-
To show these standards we will think about carbon monoxide (eq.4) and azide anion (eq.5). For each situation the most steady standard structure is on the left. For carbon monoxide, the extra holding is a higher priority than charge division.
-
Moreover, the twofold fortified design has an electron lacking carbon particle (valence shell sextet). A comparable weakening component is available in the two azide standard structures on the top column of the section (three bonds versus four bonds in the left most construction). The base line pair of designs have four bonds, however are undermined by the high charge thickness on a solitary nitrogen particle.
Every one of the models on this page show a significant limitation that should be recalled when utilizing reverberation. No iotas change their situations inside the normal primary system. Just electrons are moved.
Nuclear and Sub-atomic Orbitals
A more nitty gritty model of covalent holding requires a thought of valence shell nuclear orbitals. For second time span components like carbon, nitrogen and oxygen, these orbitals have been assigned 2s, 2px, 2py and 2pz. The spatial circulation of electrons possessing each of these orbitals.
1. The valence shell electron setup of carbon is 2s2, 2px1, 2py1 and 2pz0. In the event that this were the arrangement utilized in covalent holding, carbon would simply have the option to shape two bonds. For this situation, the valence shell would have six electrons-two short of an octet.
2. Notwithstanding, the tetrahedral constructions of methane and carbon tetrachloride show that carbon can frame four identical bonds, prompting the ideal octet. To clarify this covalent holding, Linus Pauling proposed an orbital hybridization model in which all the valence shell electrons of carbon are rearranged.
Cross breed Orbitals
To clarify the construction of methane (CH4), the 2s and three 2p orbitals are changed over to four identical cross breed nuclear orbitals, each having 25% s and 75% p character, and assigned sp3.
These mixture orbitals have a particular direction, and the four are normally arranged in a tetrahedral design. In this way, the four covalent obligations of methane comprise of shared electron sets with four hydrogen particles in a tetrahedral setup, as anticipated by VSEPR hypothesis.
Atomic Orbitals
Similarly as the valence electrons of particles possess nuclear orbitals (AO), the common electron sets of covalently fortified iotas might be considered as involving atomic orbitals (MO). It is advantageous to rough sub-atomic orbitals by joining or blending at least two nuclear orbitals.
-
As a rule, this blending of n nuclear orbitals consistently creates n sub-atomic orbitals. The hydrogen atom gives a straightforward illustration of MO arrangement.
-
In the accompanying chart, two 1s nuclear orbitals consolidate to give a sigma (σ) holding (low energy) sub-atomic orbital and a second higher energy MO alluded to as an antibonding orbital. The holding MO is involved by two electrons of inverse twist, the outcome being a covalent bond.
-
The documentation utilized for sub-atomic orbitals matches that utilized for nuclear orbitals. In this way, s-orbitals have a round evenness encompassing a solitary core, while σ-orbitals have a barrel shaped balance and include (at least two) cores.
-
On account of connections between second time frame components, p-orbitals or crossover nuclear orbitals having p-orbital person are utilized to shape sub-atomic orbitals. For instance, the sigma sub-atomic orbital that serves to security two fluorine iotas together is produced by the cross-over of p-orbitals (section An underneath), and two sp3 half and half orbitals of carbon might consolidate to give a comparable sigma orbital.
-
At the point when these holding orbitals are involved by a couple of electrons, a covalent bond, the sigma bond results. Despite the fact that we have disregarded the leftover p-orbitals, their consideration in a sub-atomic orbital treatment doesn’t prompt any extra holding, as might be shown by enacting the fluorine relationship outline beneath.
-
One more sort of MO (the π orbital) might be shaped from two p-orbitals by a parallel cross-over, as displayed to a limited extent An of the accompanying chart.
-
Since bonds comprising of involved π-orbitals (pi-bonds) are more fragile than sigma bonds, pi-holding between two molecules happens just when a sigma bond has been set up. Hence, pi-holding is for the most part seen as just as a part of twofold and triple covalent bonds.
-
Since carbon molecules engaged with twofold bonds have just three holding accomplices, they require just three half breed orbitals to add to three sigma bonds.
-
A blending of the 2s-orbital with two of the 2p orbitals gives three sp2 half and half orbitals, leaving one of the p-orbitals unused. Two sp2 hybridized carbon particles are then consolidated by sigma and pi-bonds (a twofold bond), as displayed partially B.
-
The way wherein nuclear orbitals cross-over to frame sub-atomic orbitals is in reality more mind boggling than the confined models given previously.
-
These are valuable models for clarifying the construction and reactivity of numerous natural mixtures, however present day sub-atomic orbital hypothesis includes the making of an orbital relationship graph.
-
Two instances of such graphs for the basic diatomic components F2 and N2 will be drawn above when the proper button is clicked. The 1s and 2s nuclear orbitals don’t give any general holding, since orbital cross-over is negligible, and the subsequent sigma holding and antibonding parts would drop.
-
In both these cases three 2p nuclear orbitals join to shape a sigma and two pi-sub-atomic orbitals, each as a holding and antibonding pair. The general holding request relies upon the quantity of antibonding orbitals that are involved. The unpretentious change in the energy of the σ2p holding orbital, comparative with the two ruffian π-holding orbitals, is because of s-p hybridization that is immaterial to the current conversation.
-
One illustration of the benefit presented by the sub-atomic orbital way to deal with holding is the oxygen particle. Here, the relationship chart accurately represents the paramagnetic person of this straightforward diatomic compound. Similarly, the orbital relationship outline for methane gives one more illustration of the distinction in electron thickness anticipated by atomic orbital estimations from that of the limited bond model.
-
The p-orbitals in these model are addressed by red and blue hued circles or ovals, which address various stages, characterized by the numerical wave conditions for such orbitals.
Summary
At long last, on account of carbon iotas with just two holding accomplices just two crossover orbitals are required for the sigma bonds, and these sp half and half orbitals are coordinated 180º from one another. Two p-orbitals stay unused on each sp hybridized molecule, and these cross-over to give two pi-bonds following the development of a sigma bond (a triple bond).
Frequently Ask Questions
These are some questions;
1. What is the molecular shape of CH4?
Four electron pairs are distributed in a tetrahedral shape . If these are all bond pairs the molecular geometry is tetrahedral (e.g. CH4).
2.Is CH4 three-sided and planar?
Four electron sets organize themselves in space in what is called tetrahedral course of action. A tetrahedron is a standard geometrically based pyramid.
3.What is the shape of CH4?
(a) Pyramidal. (b) Trigonal planar. (c) Linear. (d) Tetrahedral.
4. How many bonds does CH4 have?
Four bonds
Methane, CH4, is a covalent compound with exactly 5 atoms that are linked by covalent bonds. We draw this covalent bonding as a Lewis structure (see diagram). The lines, or sticks, as we say, represent the covalent bonds. There are four bonds from a central carbon (C) linking or bonding it to four hydrogen atoms (H).
5.How many electrons does CH4 have?
VSEPR estimation for methane, CH 4
It just so happens, methane is tetrahedral, with 4 equivalent bond points of 109.5° and 4 equivalent bond lengths, and no dipole second. This raises two inquiries.
6. Why is CH4 not square planar?
In CH4 particle , carbon is sp³ Hybridized , so it is tetrahedral in shape . for square planar , dsp² Hybridisation is required which is preposterous in Carbon because of nonappearance of d - orbitals. In this manner CH4 can’t be square planar .
7.Which plane is are present in CH4?
Methane is a delineation of a high equality molecule, having 8 C3 hatchets, 3 C2 hatchets and 6 σ (planes); it has a spot with the tetrahedral point pack Td, as do neopentane, adamantane and nickeltetracarbonyl.
8. Which statement is correct about CH4?
Choice 2 is right. CH4 is the compound equation for methane. It is an even particle which shows tetrahedral math. It is likewise a by and large non polar particle.
9. Why can the bond angle in CH4 be greater than 90?
Methane comprises of four reinforced sets, i.e 4 C-H bonds. To limit shock, the atom takes on a tetrahedral shape, henceforth bond point becomes 109.5. with bond point of 90, the particle would not be truly steady.
10. What is the definition of molecular geometry?
Molecular geometry is the three-dimensional Sets of the atoms that constitute a molecule.
Conclusion
If anyone want to know about Ch4 molecular shape. Then, I suggest that you must read this article. Because in this article, I described all details about Ch4 molecular shape. Hopefully this article will helpfull for you.