Surface area of a cylinder

Math
1

A cylinder is a three-dimensional object and the total proportion of its surface would be referred to as the surface area of the cylinder. The word surface means the exterior part or topmost layer of something.

WHAT IS A CYLINDER?

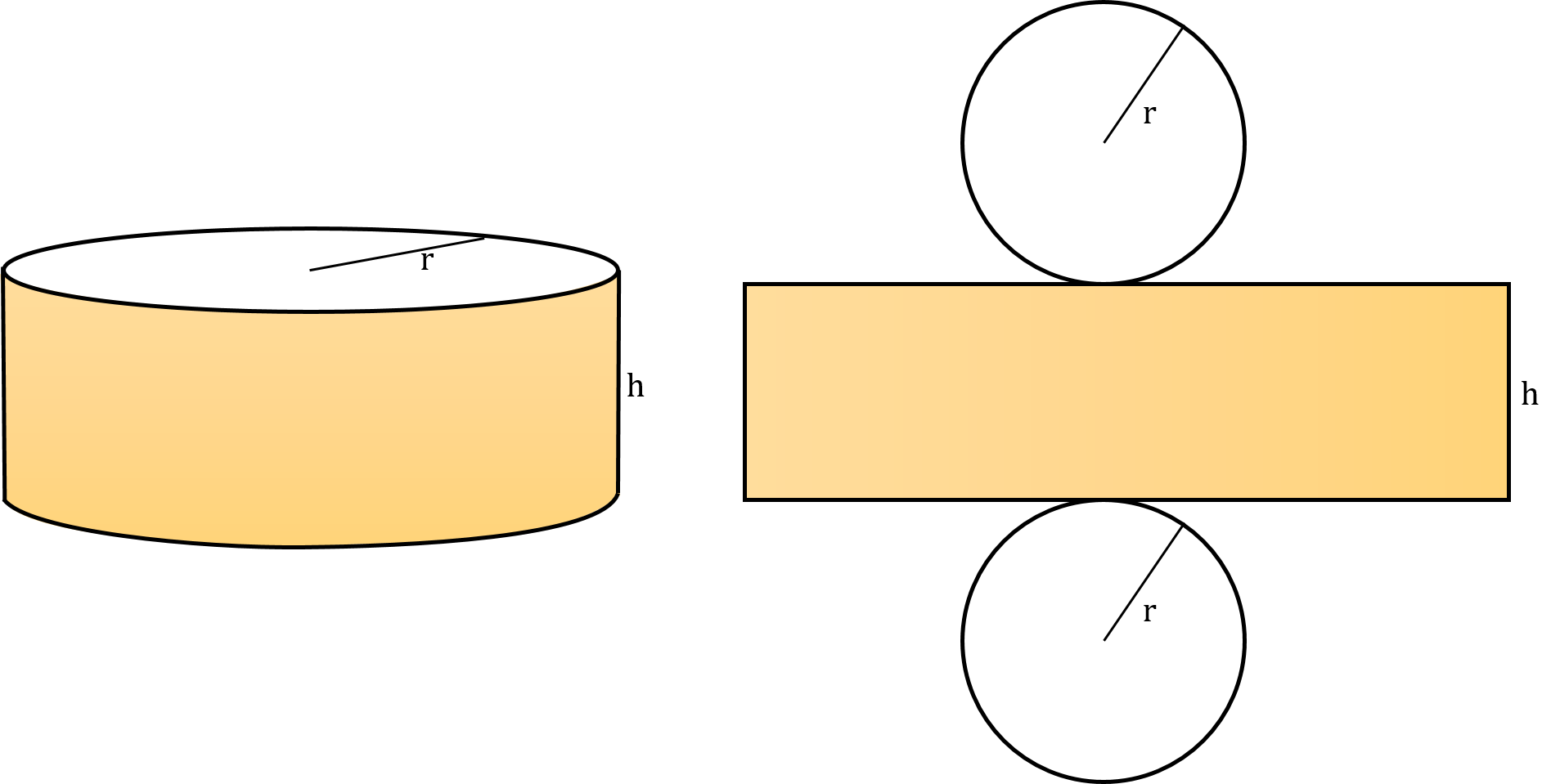
A cylinder is a three-dimensional object. It has an appearance that its length, breadth, and height are visualized. It has two round or circular bases at the edges lying parallel to each other. Both the bases are separated from each other by a distance and this distance is referred to as the height of the cylinder. The height of the cylinder lies perpendicular to the bases.

WHAT IS THE DIFFERENCE BETWEEN A CYLINDER AND A CUBOID?

A rectangular cuboid resembles a lot with a cylinder but there is a slight difference in their shapes which differentiates both of them. Both the shapes are three-dimensional and have the same orientation. Both the shapes have two bases lying parallel to each other separated by their height lying perpendicular to the bases. The thing which creates the difference is the shape of the bases as the cylinder has a circular or round-shaped base and the area between them is completely rounded and smooth but the rectangular cuboid has a quadrilateral shaped base and the area between them has edges and is not rounded and hence due to this major difference the formula for finding the surface area of both the shapes is different.

FORMULA FOR FINDING THE SURFACE AREA OF A CYLINDER:

The formula for finding the surface area of a cylinder is quite simple. All you have to do is just add the area of both the bases and the distance separating them.

As both the bases are circular, hence, to find out their area we can use the formula: (Where “r” is the radius of the circular base)

Secondly, we have to work out the area of the distance between both the bases. For this purpose we would be using the formula:

Area = length × width

(Length = circumference of the base of the cylinder or the distance around the edge of the circular base)

(width = height of the cylinder or the perpendicular distance between both the bases lying parallel)

Hence,

Length = l = 2πr

Width = b = h

Now,

Area = length × width

Area = 2πr . h

To find the total area of the cylinder now we have to add the areas of the two bases and the distance separating them.

Area of top base + Area of bottom base + area of the distance separating both the bases

πr^2+ πr^2 +2πr.h

2πr^2+ 2πrh

The surface area of a cylinder with “h” height and “r” radius is,

S = 2πr^2+2πrh (square unit)

Despite the fact that both the shapes namely cuboid and cylinder resembles a lot but the above formula for finding the surface area of a cylinder cannot be used to find the surface area of a cuboid. For finding the surface area of a cuboid the formula will be: 2lw + 2lh + 2hw (sum of the areas of all faces)

SUMMARY:

The surface area of a cylinder is the total magnitude of its outermost layer which can be calculated easily by incorporating the values the height and the radius of the cylinder in the formula: S = 2πr^2+2πrh (square unit).

WHAT IS VOLUME?

Volume is said to be the mass of the magnitude of any substance or thing or shape or simply the amount of space that is covered or occupied by any object is said to be the volume of that object.

We can calculate the volume of different geometric shapes by using the formula. But keep one thing in mind that the formula for finding the volume of different shapes would be different.

DIFFERENCE BETWEEN SURFACE AREA AND VOLUME:

Surface area and volume are two different terms having different meaning and cannot be regarded as equal or same as the surface area is something related to the exterior surface of a shape or object or anything while the volume is the total magnitude of the shape or simply the amount mass contained in the object.

Both surface area and volume of any object can be calculated by using accurate formula but keep one thing in mind that the formula for finding the surface area of a shape cannot be used to find out its volume rather you have to use a different formula for finding the volume of that particular shape.

For different shapes, we have different formulae for finding their surface areas and volumes and they cannot be interchanged like the formula for finding the surface area of a cuboid cannot be used to find the surface area of a cylinder.

FORMULA FOR FINDING VOLUME OF A CYLINDER?

The volume of a cylinder having radius “r” and height “h” can be easily calculated by incorporating both the values in the formula:

V = πr^2h (cubic unit)

We have to take the square of the radius of the cylinder and after placing all the values in the above-mentioned formula all we have to do is just calculate the product and we will get the value of the volume of the cylinder.

Dealing with different for finding their surface area we used different formulae same we will do in case of finding their volumes. For each shape, there is a slight difference in the formula for finding the volume.

Despite the similarity between cylinder and cuboid, we cannot incorporate the above-mentioned formula for finding the volume of cuboid.

For finding the volume of cuboid we will use the formula given below:

Volume = length × breadth × height (cubic unit)

Volume = l × b × h (cubic unit)

SUMMARY:

Surface area and volume are two different parameters of a geometric shape and should not be misunderstood. The formula for finding the volume of a cylinder is V = π h. For different shapes same as of surface area we have a different formula for finding the volume as well.

For a better understanding of the above-discussed formulae let us consider few examples:

EXAMPLE 1

Find the surface area and volume of a cylinder with a radius of 3cm and a height of 10cm.

DATA:

Radius = r = 3cm

Height = h = 10cm

Surface area = S = ?

Volume = V = ?

SOLUTION:

For the surface area of a cylinder:

S = 2πr^2+2πrh

S = 2 (3.14) (3)^2 + 2 (3.14) (3) (10)

S = 244.92 cm^2

For finding the volume of the cylinder:

V = πr^2h

V = (3.14) (3)^2 (10)

V = 282.6 cm^3

RESULT:

Hence the surface area of the cylinder is 244.92cm^2 and the volume is 282.6cm^3.

EXAMPLE 2

Find the surface area and volume of a cylinder with a radius of 6m and a height of 12m.

DATA:

Radius = r = 6m

Height = h = 12m

Surface area = S = ?

Volume = V = ?

SOLUTION:

For the surface area of a cylinder:

S = 2πr^2+2πrh

S = 2 (3.14) (6)^2 + 2 (3.14) (6) (12)

S = 678.24m^2

For finding the volume of the cylinder:

V = πr^2h

V = (3.14) (6)^2 (12)

V =1356.48m^3

RESULT:

Hence the surface area of the cylinder is 678.24m^2 and the volume is 1356.48m^3.

EXAMPLE 3

Find the surface area and volume of a cylinder with a diameter of 4m and a height of 8m.

DATA:

Radius = r = d/2 = 4/2 = 2m

Height = h = 8m

Surface area = S = ?

Volume = V = ?

SOLUTION:

For the surface area of a cylinder:

S = 2πr^2+2πrh

S = 2 (3.14) (2)^2 + 2 (3.14) (2) (8)

S = 125.6m^2

For finding the volume of the cylinder:

V = πr^2h

V = (3.14) (2)^2 (8)

V = 100.48m^3

RESULT:

Hence the surface area of the cylinder is 125.6m^2 and the volume is 100.48m^3.

FREQUENTLY ASKED QUESTIONS:

There is a number of questions that people often ask related to the surface area whether relevant or irrelevant to the topic. Some of the questions that are frequently asked are discussed below:

1. How do you calculate the surface area of a cylinder?

Answer: Surface area is the total proportion of the outermost part of anything. For finding the surface area of the cylinder one t know the radius and height of the cylinder and then all you have to do is just put the values in the formula: S = 2πr^2+2πrh (square unit)

2.What are the TSA and CSA of a cylinder?

Answer: CSA (Curved Surface Area) is the area of the curved part or the distance between the two circular bases of the cylinder and TSA (Total Surface Area) or simply the surface area is the area of both the circular bases as well as the CSA (Curved Surface Area).

3. What is the formula of diagonal of a cylinder?

Answer: Diagonal is a line that joins the two opposite corners of a shape. In the case of a cylinder, the diagonal can be defined as a line segment that acts as a hypotenuse in a right-angled triangle taking the diameter of the cylinder as base and height as perpendicular of the right-angled triangle. To find the exact measurement of the diagonal we will use the formula =(diameter^2+height^2)^1/2.

4. What is the curved surface of a cylinder?

Answer: A cylinder is a three-dimensional object. It has an appearance that its length, breadth, and height are visualized. It has two round or circular bases at the edges lying parallel to each other. Both the bases are separated from each other by a distance and this distance is referred to as the height of the cylinder. The height of the cylinder lies perpendicular to the bases and is curved throughout its length and hence it is referred to as the curved surface of the cylinder.

5. What is the surface area of a circle?

Answer: Circle is a two-dimensional object and the total area or space covered by the circle is the surface area of the circle.

6. How do you solve surface area and volume problems easily?

Answer: For different shapes, we have different formulae for surface area and volume respectively and by incorporation the correct measurements into the appropriate formula and by performing mathematical calculations correctly we can easily calculate the surface area and volume of any shape we are asked to work on upon.

7. What are surface area and volume?

Answer: Surface area and volume are two different terms having different meaning and cannot be regarded as equal or same as the surface area is something related to the exterior surface of a shape or object or anything while the volume is the total magnitude of the shape or simply the amount mass contained in the object.

Both surface area and volume of any object can be calculated by using accurate formula but keep one thing in mind that the formula for finding the surface area of a shape cannot be used to find out its volume rather you have to use a different formula for finding the volume of that particular shape.

8. Is surface area equal to volume?

Answer: Surface area and volume are two different terms having different meaning and cannot be regarded as equal or same as the surface area is something related to the exterior surface of a shape or object or anything while the volume is the total magnitude of the shape or simply the amount mass contained in the object.

9. What is the total surface area of a cube?

Answer: The total surface area of a cube can be calculated easily by using the formula= 6. (Where “a” is the abbreviation for each side of the cube) contrary to the square the cube is a three-dimensional shape but it’s all sides or edges are of equal length.

10. What is a cube formula?

Answer: Cube means we have to multiply that specific digit by itself three times like a cube of 3= (3)^3=3×3×3= 27.

CONCLUSION:

It is clear that surface area and volume of any shape are two different things having different formulae and units. The two shapes namely cylinder and cuboid and cylinder are not exactly the same they have a slightly different geometry. For finding the surface area and volume of a cylinder we must know the radius and height of the cylinder and by incorporating both the values in the respective formula we can easily calculate both the values.

READ RELATED ARTICLES:

Volume Of A Cylinder

What is the formula for the surface area of a cylinder?

Length and Width

Volume

Specific volume

2

Since a cylinder is closely related to a prism , the formulas for their surface areas are related.

Remember the formulas for the lateral surface area of a prism is phph and the total surface area is ph+2Bph+2B . Since the base of a cylinder is a circle, we substitute 2πr2πr for pp and πr2πr2 for BB where rr is the radius of the base of the cylinder.
So, the formula for the lateral surface area of a cylinder is L.S.A.=2πrhL.S.A.=2πrh
If you have ever seen a can of soda, you know what a cylinder looks like. A cylinder is a solid figure with two parallel circles of the same size at the top and bottom. The top and bottom of a cylinder are called the bases. The height hh of a cylinder is the distance between the two bases. For all the cylinders we will work with here, the sides and the height, hh , will be perpendicular to the bases. A cylinder has two circular bases of equal size. The height is the distance between the bases.
An image of a cylinder is shown. There is a red arrow pointing to the radius of the top labeling it r, radius. There is a red arrow pointing to the height of the cylinder labeling it h, height.
Rectangular solids and cylinders are somewhat similar because they both have two bases and a height. The formula for the volume of a rectangular solid, V=BhV=Bh , can also be used to find the volume of a cylinder.
For the rectangular solid, the area of the base, BB , is the area of the rectangular base, length × width. For a cylinder, the area of the base, BB, is the area of its circular base, πr2πr2. The image below compares how the formula V=BhV=Bh is used for rectangular solids and cylinders. Seeing how a cylinder is similar to a rectangular solid may make it easier to understand the formula for the volume of a cylinder.
In (a), a rectangular solid is shown. The sides are labeled L, W, and H. Below this is V equals capital Bh, then V equals Base times h, then V equals parentheses lw times h, then V equals lwh. In (b), a cylinder is shown. The radius of the top is labeled r, the height is labeled h. Below this is V equals capital Bh, then V equals Base times h, then V equals parentheses pi r squared times h, then V equals pi times r squared times h.
To understand the formula for the surface area of a cylinder, think of a can of vegetables. It has three surfaces: the top, the bottom, and the piece that forms the sides of the can. If you carefully cut the label off the side of the can and unroll it, you will see that it is a rectangle. See the image below.
By cutting and unrolling the label of a can of vegetables, we can see that the surface of a cylinder is a rectangle. The length of the rectangle is the circumference of the cylinder’s base, and the width is the height of the cylinder.
A cylindrical can of green beans is shown. The height is labeled h. Beside this are pictures of circles for the top and bottom of the can and a rectangle for the other portion of the can. Above the circles is C equals 2 times pi times r. The top of the rectangle says l equals 2 times pi times r. The left side of the rectangle is labeled h, the right side is labeled w.
The distance around the edge of the can is the circumference of the cylinder’s base it is also the length LL of the rectangular label. The height of the cylinder is the width WW of the rectangular label. So the area of the label can be represented as
The top line says A equals l times red w. Below the l is 2 times pi times r. Below the w is a red h.
To find the total surface area of the cylinder, we add the areas of the two circles to the area of the rectangle.
A rectangle is shown with circles coming off the top and bottom.
The surface area of a cylinder with radius rr and height hh, is
S=2πr2+2πrh
To estimate the surface area of a cylinder, you need to visualize it as a net. It is as if you open the cylinder just like a carton box and then flatten it out. Use your imagination! And what will you get? The answer is that a right circular cylinder consists of two circles and one rectangle, as you can see it in the figure below.
How to find surface area of a cylinder - a picture of unfolded cylinder
Therefore, the base surface area of a cylinder equals two times area of a circle with the radius r, and the lateral surface area of a cylinder is the area of a rectangle. The first side of this rectangle is the height of the cylinder h and the second is the circumference of the base 2 * π * r. Now, after we know how to find the surface area of a cylinder, let’s derive appropriate formulas for the surface area of a right circular cylinder. To calculate the base surface area, you need to compute the area of a circle with the radius r. But remember that every cylinder has two bases! Thus, you need to multiply it by two:
base_area = 2 * π * r²
Estimation of the lateral surface area is even easier. Because the area of a rectangle is the product of its sides, we can write that:
lateral_area = (2 * π * r) * h,
where

  • 2 * π * r is the circumference of the base circle,
  • h is the height of a cylinder.
    Finally, the total surface area of the cylinder formula is simply the sum of the base surface area and the lateral surface area:
    total_area = base_area + lateral_area,
    or total_area = 2 * π * r² + (2 * π * r) * h,
    or total_area = 2 * π * r * (r + h).
    With our surface area of a cylinder calculator, you can perform all the calculations in many different units. If you want to learn more about area unit conversion, check out our area converter now! In the advanced mode of this calculator you can also calculate the volume of a cylinder. The interesting fact is that every cylinder with the same heights and base areas has the same volume. It doesn’t matter whether it is a right or oblique cylinder.