Mathematics is the number of games. Is mathematics easy? The answer is both yes and no. However, it depends on the individual’s capacity and hard work
Tips to solve mathematics problems easily
Do you find yourself becoming increasingly perplexed when you glance through your child’s math textbook? Don’t be concerned — you are not alone! However, there is no need to be concerned; the principles and ideals that our children are learning in primary 1 and 2 arithmetic are the same. Said, instructional techniques have progressed from what we were accustomed to.

-
Solving past paper questions is a good way of practicing for examinations and getting those vital marks. Remember to be 100% accurate as you will not get any defects if you make a mistake - nothing ventured, nothing gained!
-
If it’s an AS or A2 maths exam and the question requires calculations, draw diagrams wherever possible l speed up your working and can sometimes help you find the answer.
-
If it’s an exam, after drawing your diagram,s use elimination to try and reduce the number of unknowns - often there are equations containing several variables which can cancel each other out enabling you to solve for fewer unknowns than there were originally
-
Efficiently using pen and paper is vital. Draw diagrams as neatly as possible, so the question is easy to follow, and you can ensure that your calculations are accurate
-
In an exam, there will be more marks for a better answer than a good one - always attempt to give the best solution even if it takes a bit of working out
-
If it’s a pure maths paper, then don’t ignore those questions from other syllabuses such as mechanics or statistics unless they do not carry any marks
-
Always read through all parts of a question carefully - even if you think you’ve worked something out fully, make sure that you re-read the question before marking your answer sheet because often this can mean finding another way of looking at things which could lead to further marks
-
If its a maths problem, keep checking that any formulae you use are correct and appropriate for the question
-
In an exam, don’t put down your workings in the spaces provided on the answer sheet or between questions - if you make a mistake or change your mind, erase it and start again; this is because once the paper has been awarded and checked errors cannot be corrected and marks may be deducted (you can always go back to your rough work though)
-
When tackling multiple-choice questions, read through all of the options before attempting to answer anything. Read each option carefully for clues for what type of answer they’re looking for. Attempt each possible solution in turn until it works out. Remember, there should only be one correct answer.
-
Asking for help does not mean you’re thick! If it takes somebody to point out the obvious for you to realize something, then that shows how well they know you - use this support network
-
Learn your formulae but don’t rely on them, also learn to solve problems without needing complicated methods; often, less complex ways are quicker and more accurate.
-
Always show your work even if it’s wordy or badly drawn) because part of the marks might come from seeing an efficient method of solving the problem
-
Remember there is no substitute for practice - do past papers, mark them yourself and analyze why specifics were awarded higher marks than others; demonstrated the ability to solve the problem using proper mathematical techniques is more important than achieving ‘the right answer’
-
Use appropriate units! This seems like an obvious point, but no marks are deducted for having the wrong units (which might lead you on to use inappropriate formulae)
-
Also, on calculations - make sure any numbers used as divisors or multipliers in your answer are indicated as such by separating them with a colon, e.g. 3:4 would mean three 4/10ths; x: y * z means xy times z; .5 means 1/2; = means equals; ~ means approximately equal to; > and < mean greater than and less than respectively and ≈ ∝ mean roughly equal to and proportional to respectively
-
If you’re allowed a calculator, then use it! As long as your arithmetic is correct and you spot any mistakes in your work during the calculation process, there shouldn’t be a problem, but if you make several mistakes that aren’t spotted until later on (e.g. an incorrect answer) or don’t show all of your workings, marks may be docked
-
Don’t panic! Often how well you think under pressure is more critical than what mark you would have got if you’d left yourself enough time
-
Always check that the units cancel out correctly when doing calculations - this one’s a killer because most mistakes happen at this stage
-
Here’s a tip which I don’t know how well it works because in my time at school, we didn’t have calculators, but apparently in a timed exa, m you can rapidly multiply fractions by ten by moving the decimal point to the right and adding one if the number is odd or nothing if it’s even.
Of course, if you have a calculator, this tip won’t be of much use!
-
When rearranging formulae by multiplying or dividing both sides by a particular factor, make sure you also multiply or divide everything else in the equation by the same factor - it’s incredible blue how many marks you can lose doing this
-
Make sure your calculations are done in order from left to right, and any brackets are correctly paired
-
This is not just for exams - when writing down formulae, always clearly label each type of quantity with its appropriate letter, e.g. V = not would be Volume equals a number of liters multiplied by density which must be expressed in kg/m3. Also, make sure all symbols used correspond to their correct definitions, e.g. don’t write v for volume, T for time, etc
-
Another tip which applies not only in exams but generally - wherever you see a mistake, do it yourself and make sure there isn’t one there too!
-
Isolate your variables whenever possible - if you have an equation with lots of letters on the right-hand side, you can solve it more quickly by moving terms containing unknowns to the other side until they’re isolated on one side of the equals sign, e.g. 5x + 10y = 50 becomes x+y = 20 because everything containing x or y has been moved across to the left leaving just 20 on that side
-
Equations are generally more accessible solved by isolating the unknowns on one side of the equals sign and working backwards, so start by moving all terms containing known quantities to one side of the =
-
Be careful when using ‘back substitution’ - replacing the values you’ve just found into your original equation could result in errors if it turns out that any step along your route was (this happened to me once, but luckily I spotted the mistake!)
-
If you’re given twequationsos with two variables, es try graphing them on a pair of axes; this will often give you helpful information about how to solve them much quicker than trying to do everything using algebra
-
The same goes for inequalities - plotting them on an appropriate number line should make it easier to solve, e.g. if you’re given x > 2 and y < 3, plot the corresponding point (x,y) on a number line
-
If you’re allowed to use a calculator, then try ■■■■■■■ polynomials (e.g. y = ax2 + bx + c ) or functions of more than one variable (e.g. y = f(x,z) ) to your data; this is much quicker than using algebra and will often produce a more accurate answer
-
A lot of the errors I made at school were my fault because they involved working out something incorrectly and then hitting a wrong key on my calculator - if you’re going to use a calculator, make sure you understand how it works and how to do things correctly
-
If possible, always go for an answer that’s shown as simply as possible - e.g. 22/4=5 is better than 22/4= 5 1/2
-
In exam questions involving percentages, find what percentage each number is of the whole quantity before doing anything else, e.g. in an advertisement selling mobile phones, the ad claims 50% off all handsets costing £200 or more. If you want to buy one, what’s the cheapest handset you can get?
-
The most straightforward way of solving most equations containing fractions is to cross multiply - if x/y=a/
b then (x)(b) = (y)(a)
-
When using a calculator, it’s essential to be clear about your rounding convention, e.g. two decimal places or 3? Also, check that your answer makes sense; if you’re finding an average, don’t forget to look at the figures adding up to that average
-
If you’re adding, subtracting or multiplying decimals take care with signs + - x ÷ (e.g… 4 567 + 1 978 = 5716 instead of 5750!)
-
If you’re asked to find half or double something (e.g. double 572), remember that the answer probably won’t be exact; use your knowledge of rounding conventions to make sure your final answer is as close as possible
-
Make sure you know what units to use for different quantities - don’t write m/s if you mean km/h
-
Don’t forget how indices work, e.g. a 2 = a × a = a3. Also, whenever multiplying or dividing fractions with an unknown in them, try cancelling the known quantity first before doing anything else, e, e.g. 3 4 ÷ x=1 three ÷ x= 1
Summary
In trigonometrical questions, it’s often much easier to draw a picture and then use a calculator or a SOHCAHTOA table to solve the problem, e.g. sin x = opposite hypotenuse
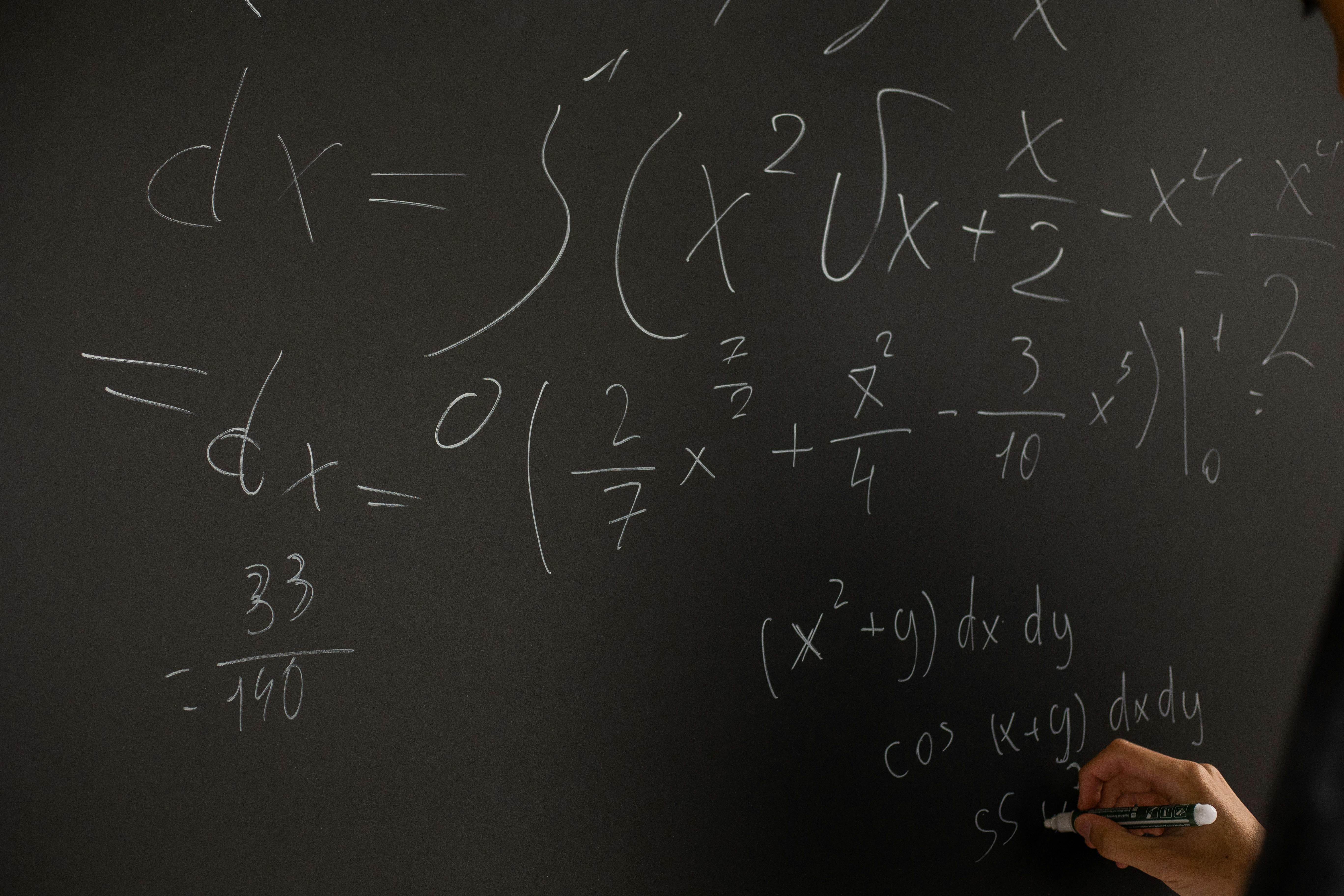
How to refocus during examinations?
Here are some easy yet effective ways to relax and refocus during examinations.
Take frequent breaks.
Some students may find it counterintuitive to take a break when they have so little time left to finish their revision. Study breaks, on the other hand, are crucial for allowing your brain to relax and recover. Math may be a mentally taxing topic at times. After a period of solving arithmetic problems, a person’s focus begins to wane substantially. You may not experience weariness immediately, but it has an impact on your problem-solving productivity and memory. You may become stopped on a fundamental math issue due to a ‘mental block induced by tiredness.
Exercise
When we tell students to take time out to exercise, many of them look at us incredulously. However, one of the most excellent methods to turn trigonometric math functions is to exercise. Exercise improves our mental sharpness, enhances our energy and has a favorable effect on our mood. The good news is that you don’t need much exercise to get these effects; go for a 20-minute brisk stroll and then return to your integration math work.
Get plenty of water.
One of the most crucial but frequently ignored factors is staying hydrated. Drinking enough water throughout the test has two advantages. First, it allows you to focus better. And, because drinking water helps your liver do its job better (by eliminating toxins from your body), it also helps keep you healthy throughout this critical period.
Avoid “burning the midnight oil.
Many students study late into the night to complete as much work as possible. However, looking late at night reduces your mental alertness the next day and lowers your total productivity. You’ll start making casual errors on simple math calculations.
Summary :
Getting a distinction in math (or any subject) is fantastic, but keep in mind that there is more to life than just high grades. Even if you perform poorly on a specific exam, it is not the end of the world. There will be many more chances to express yourself and achieve later in life. In a nutshell, get in there, do your best, and stay focused.
Ways to make maths learning fun A research-based study
“'ve had the same 6th-grade teacher for sixix years. She’s taught me more than any other class I’ve ever taken, and I know it’s because she’s making math fun instead of trying to make us like the subject.”
This quote has been taken from an article written by Geraldine Woods in which she discusses how mathematics is often viewed as a complex, tedious,
and dull subject at school. This quote sums up her whole article about why mathematics should be taught differently so children will enjoy learning it
According to the author, there are two main ways to make maths more appealing :
-
The first way is “to abandon formal instruction…”
-
The second way is that teachers need to be creative, making connections with real life
According to the author, “abandoning formal instruction” here means that kids are not forced to learn things in a particular order. If they make mistakes, it is permitted. This will hopefully make them feel more confident about what they are doing and therefore increase their chances of success.
The second way of making mathematics more appealing is to make connections with real-life; according to the article, this should include money (for example, shopping), time (what time is it ?), and measurement (height, etc.). These subjects can be fun because students connect abstract mathematics with something tangible in their lives. This connection makes learning more accessible because they know why they need to learn these topics. For example, if you want to go shopping, you need to know how much money you have and how much things cost.
Another way math can be made more appealing is by making it practical; for example, "if I went into a fast-food restaurant and ordered a burger, fries and a drink, k the total bill would be $3.75 if each item costs 75 cents.
In this case, we see that there is no formal instruction,n but the student has used their initiative to work out the price of his meal (85). This is also a real-life connection because he might fast food fast-food one day.
According to an article written by Jennifer Serravallo entitled “Making Math More Fun”, there are five ways in which mathematics can become more fun :
-
According to her, the first way is to set challenging goals and let students explore
-
The second way is for teachers to “redesign lessons so that they are more relevant, real-world, visual and interactive”
-
Another option is to connect mathematics with things in the outside world, such as careers. For example, engineering jobs need math skills when it comes to architecture. This gives children a goal and reason why they should learn maths.
-
The fourth way, according to Cavallo, is that teachers need to be creative with activities and top,ics, especially if they find students don’t like certain areas of mathematics. For example, ratios can be made out of anything. One example is that drawing a balance fraction is more appealing because students can see the actual picture.
Summary:
The final w, a, y, according to Serravallo is to make math fun and interesting for students by including art, music, and multimedia. The idea behind this Is that child-like these subjects, and if they can connect them to maths, it would be more appealing to them.
Tips For Maths Teachers
Here we present some tips and tricks that mathematics teachers should know and apply to their work:
-
When you first enter your classroom, look at it as a first time visitor. What do you see? Maybe the tables are too small for students to work well, or there’s no marker board or no responsibility chart posted. Make sure that your classroom is set up for success.
-
Set high expectations with realistic goals that build self-esteem through team building activities.
-
Try using different desks/tables in your class, so every student has equal space and access to all equipment.
-
Use seat belts! Make sure each student has them on when they are working at their desk/table because sometimes this can prevent students from falling when they are in movement.
-
Every lesson should have a clear objective which you can measure by guiding questions or even just observation. If there’s no objective, it doesn’t matter what you teach.
-
Keep group sizes small so that instruction time is maximised to support all learners.
-
Evaluate the quality of student work, not the quantity. Set up quality control checkpoints along the way at every opportunity; this will lead to success for your students and help them gain confidence in their ability to learn math!
-
Avoid using worksheets at all costs unless you want your classroom to be like a factory stamping out products (not people). The loss of problems through worksheets is irreversible.
-
Use manipulatives. It is more important for students to have the ability to use materials than it is for them to “do their math” by looking at a paper.
-
When introducing new material, stop periodically and ask students questions that require higher-level thinking skills. Students should be doing all of the talking in class, not you! If you’re doing most of the talking, something needs to change. Ask yourself what your students are learning from this lesson. If you don’t know, or if they aren’t learning much beyond how to follow directions - find another way!
-
Identify strong readers early on to help struggling readers with decoding words before proceeding with regular instruction group read-aloud within small groups.
-Teach in mixed ability groups. It’s okay to group students by ability if they complete an inquiry task, but make sure to switch the grouping around when needed throughout the year, so all students get exposure to different levels of thinking.
-
Make it ok for kids not to know all of the facts/formulas/strategies; mainly, they are guided through a problem-solving process that requires them to draw on their prior knowledge and use reasoning skills to succeed at math! This often means working with several different strategies or representations before arriving at an answer - this is deep learning, where there’s no shortcut route because being proficient at math takes practice!
-
Pair struggling students that are not in the same group when appropriate.
-
Focus on one math concept at a time and do it well (put all of your energy into the lesson at hand), moving to another topic only when you see your students gaining mastery in current work. This is how you avoid overwhelming them with too much new information in one lesson.
-
Give every student an equal chance to be successful by always including some targeted remediation for any student that seems disengaged or disinterested during class time - this could mean being pulled out of the regular classroom environment for small group tutoring during choice time/recess/lunch hour/early dismissal, whatever works best for your school schedule!
-
Teach math in a way that’s interesting, relatable, real-life, and engaging for students! This means modelling strategy use during class time with your students - you don’t have to be the only one who knows how to solve a problem.
-
You can’t teach if your students are not paying attention. If it gets boring, change things up until you get engagement again.
Math is about using patterns, problem-solving skills, and working together, which are all excellent life skills to learn when one is young. Math should be fun, and when it becomes so, children will want to know more. Forcing them won’t work unless they are ready or motivated to do so.
Teachers choose what activities they do in the classroom by looking at their objectives. They should not limit themselves to the traditional lesson plans filled with worksheets and activities that do not motivate students.
Math is best taught one skill at a time, as this can be done without overwhelming children or making them bored with all of the new information they are being given. When a child understands one concept well, teachers need to build on what has been learned so that children do not feel behind compared to others in their class. Teachers should look for opportunities throughout the day to understand and reteach needed skills when necessary to ensure each student feels successful.
Every child deserves an equal chance to succeed, which means recognizing help with learning math. Some students need small groups while others, on the other hand, may need individualized attention after school for an hour or more on some days.
Math is best taught in a way that engages students, meaning it should be presented in ways that are interesting and relatable to them. Math problems should not just use numbers but instead include real-life situations with things children know about, encouraging them to think deeply of new possibilities they have never considered before.
Summary:
Math lessons should be thought out carefully so new concepts fit into the everyday math behaviour of students by allowing for opportunities where the practice of skills learned can take place within different activities both individually and collaboratively. By doing this, children will not get bored of the same old worksheets they see in their textbooks but will instead feel a sense of excitement and satisfaction with the work they do.
Frequently Asked Questions
Here are some questions that people ask
1. What are the Possible Obstacles that Children May Face and How They Can Be Overcome?
Math word problems may be complex because they need more than answering the question. Not only must your youngster read, but they must also determine which mathematical
The operation to apply and then concentrate on solving the problem as a whole.
A youngster who excels in math may struggle with problem sums as well.
.
2. Can Reading Difficulties hinder solving math problems?
One of the most challenging problems youngsters encounter when answering problem-solving questions is their inability to understand what the question is asking. A compared youngster with more important language skills, a child with poor language ability will fail to understand the long problem amounts.
3. How to solve reading difficulties?
To see whether this is an issue, read the question aloud to your kid. If your child can answer the question when read aloud to him but not when he is allowed to read on his own, the issue is one of reading comprehension.
Speak with your child’s instructor and inquire about the possibility of having word problems read aloud on occasion.
4. How does Choosing keywords help?
In Maths problem sums for primary 1 and 2, several keywords help youngsters in answering the questions. Learning to recognise important words is critical in determining which mathematical operation to build a number sentence to solve the total. A substantial reader may falter at this point because he must transform a brief text into a numerical phrase. For a youngster, this needs a lot of brain processing.
To address this difficulty, work with your students to identify essential terms in a word problem. They must understand that key phrases are just words that provide meaning to the numerical statement.
5. Why is Taking notes vital during mathematics?
As soon as a teacher starts writing things on the board/whiteboard - start taking notes! Why are they telling us this? How does this relate to other stuff we have learned? Write everything down; otherwise, it will be gone in an instant when you need it most. Multiply what you write down by ten because that’s how long it will take you to actually understand it later on when revising. Don’t write too much though, you might not need it all!
6. why to Do past papers every year?
This is the only way to know if you are doing well enough or if you really do understand what’s going on. It will tell you where your weaknesses are and make sure they don’t stay that way! If there isn’t one for your particular subject then ask around at other schools. Sometimes they can be found online via Google - just try to avoid any that may have been illegally obtained. Just remember that past papers aren’t exactly like the real exam so don’t panic if something seems incredibly different - anything could be in the real thing…
7. How essential is understanding?
Don’t just write an answer to a question because your teacher told you to or it’s easy. Make sure you can explain tricky concepts/questions easily and if not then look back at (1) and (2) - you’ll be surprised how quickly things can disappear from memory! Also, make up example questions about everything you learn. A good tip is to ask yourself “What would I like to be able to do with this? What would make me more employable?” This will ensure that the information has sunk in rather than just being present temporarily before disappearing forever.
8. Is Revision essential?
Try using mind maps and sticky notes to connect ideas together in different ways. Make sure you read through your notes at least once a week so the information doesn’t disappear completely. If it isn’t interesting, then just say to yourself “What would I like to be able to do with this? What does this mean for me in the future?” This simple mental shift will keep you awake and much more likely to remember what you’re revising!
9. How much does Staying Positive help?
Don’t panic - if you’re panicking then everyone else is too and that’s not good for anyone. Just remember: You know more than you think and practice makes perfect! Focus on your strengths and make up questions about them - put yourself in the examiners’ shoes; how would you mark this?
10. How should the ideal learning process be?
The learning process begins with helping pupils fall in love with the topic. We feel that pushing a pupil is never a good solution. We aim to show them the lighter side of the complicated subject by using real-life examples, factual facts, diagrams, and other visual aids. The children are then encouraged to try solving arithmetic problems on their own to improve their foundation.
Conclusion
In conclusion we see that everybody agrees on one thing: Mathematics should be taught differently so children will enjoy learning it. This can be achieved in many ways such as making connections with real life, using practical activities, or just generally giving children freedom when they are trying to solve problems. If we manage to successfully incorporate these ideas into our teaching we might actually find children who want to stay in maths for longer than five minutes.