Linear Pair: Definition
A pair of adjacent or supplementary angles. Adjacent means next to the first one supplementary means the measurement of the angles and add 180 degrees or it’s equal.
Adjacent and Supplementary
As mentioned above, adjacent points are angles that are close to one another. In the event that you are sitting close to somebody in class or on the transport, you could say that you are contiguous to them. All the more explicitly, nearby points share a vertex and have a typical side.
Advantageous points are any pair of points that add to rise to 180 degrees. Suppose you need to make a specific measure of cash every month to take care of the entirety of your bills, yet you just make a bit of that cash at your normal work. You may wind up searching for extra work to enhance your ebb and flow income. Your two positions add to approach the sum expected to take care of your bills similarly that two supplementary angles add to rise to 180 degrees.
Lines
Another significant fact is that a line estimates 180 degrees. Along these lines, a couple of nearby, valuable points makes a line. Have you at any point seen how the name parts with it? A 'line-ar pair is a couple of points that make a line.
Application
You may experience issues that request that you address for the missing point utilizing a direct pair. As we have examined, a straight pair amounts to an equivalent 180 degrees. Assuming you know the proportion of one of the two points, you can deduct that action from 180 degrees to get the proportion of the other point.
For instance, suppose that point An actions 75 degrees. What is the proportion of point B if this is a straight pair?
Keep in mind, you can’t expect to realize estimations dependent on the photos that may show up in your coursebook or on a test. You can just work dependent on the data that is given. This powers you to apply the ideas you have learned as opposed to depending on a visual.
Solution
180-75=105
so, angle B measure 105 degrees
8 Real-Life Examples of Linear Pair
Although the fact that science may be viewed as one of the exhausting subjects to many, you would get astounded to realize that it has many fascinating ideas to encounter with regards to our day-by-day life. One such gem of arithmetic is the ‘Straight Pair’ of points. Direct Pain is a bunch of two points that are contiguous one another, framed by two meeting lines, and the proportion of straight points ought to be 180 degrees. In our day-by-day schedule, we face a few circumstances where the idea of Linear Pair of points is applied. Regardless of whether we don’t see, there are numerous things around us that structure the piece of linear pair.
The conditions of a linear pair angle are:
-
Adjacent to each other
-
Have a common vertex
-
Non-common side must make a straight line or sum of angles must be 180 degrees.
we all might have would have imagined that the Linear Pair has no presence, all things considered. It’s simply hypothetical work. In any case, there are a lot of models in our day-by-day life, which proposes the contribution of Linear sets of points. Thus, we should talk about some genuine instances of linear pair in detail.
1. A ladder placed against the wall
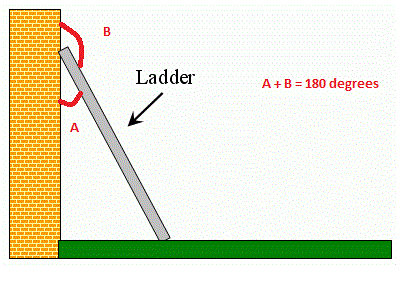
A ladder placed set against the divider is a genuine illustration of Linear Pair. Here, the ‘point A’ shaped by putting the stepping stool against the divider is contiguous ‘point B.’ Both the points framed have a typical vertex and the entirety equivalent to 180 degrees.
2. Hands of Clock
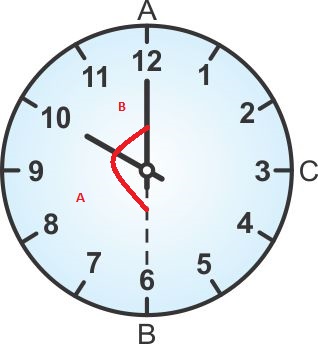
Here also, the angle An and B framed by the hands of the clock are contiguous one another, have a typical vertex, and the amount of both the points is equivalent to 180 degrees.
3. Slices of Pizza

By and large, nobody would consider stuff like arithmetic while appreciating pizza with companions. However, in the event that we see the convergences of pizza, we would see the presence of Linear Pair points. Along these lines, next time when you go to a pizza party remember to salute the Linear Pair of points.
4. Scissors
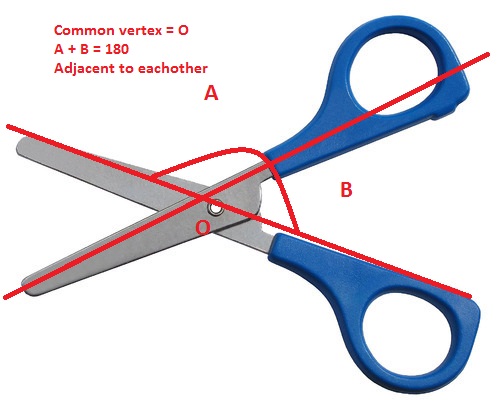
Some scissors are a classic example of Linear Pair of points, where the flanks of scissors, which are nearby one another and have basic vertex O, structure a point of 180 degrees.
5. Electric Pole
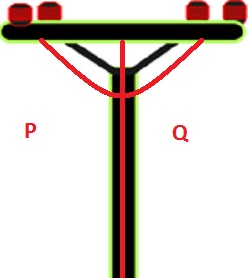
An electric post is likewise a genuine example of linear pair. The points P and Q qualify every one of the conditions to be considered as a Linear Pair.
6. Justice Balance
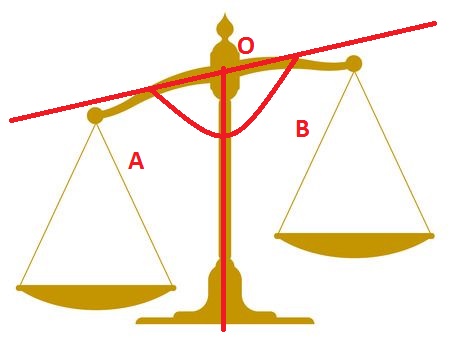
Another motivation to be appreciative of the Linear Pair of points is that it is engaged with conveying equity; as the points framed in an equity balance machine are only the Linear Pair of points.
7. T-Junction
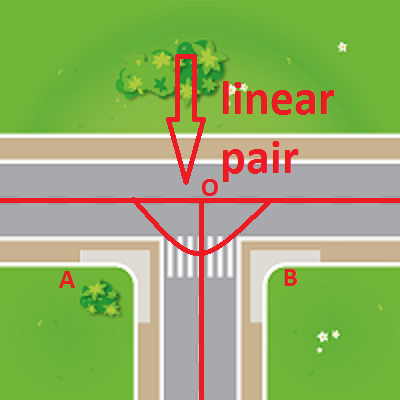
At whatever point you go for a drive, remember to see the Linear Pair of points framed at the T-intersection.
8. Chopping Board
You would be astounded to realize that the Linear Pair of points is additionally framed on the hacking board. In this way, the following time you see your mom working in the kitchen and hacking vegetables to make tasty dishes for you, remember to see the Linear Pair of points framed on the cleaving load up.
Linear Pair Of Angles
linear pair of points are shaped when two lines cross each other at a solitary point. The points are supposed to be directly on the off chance that they are neighboring each other after the convergence of the two lines. The amount of points of a direct pair is consistently equivalent to 180°. Such points are otherwise called advantageous points. The nearby points are the points that have a typical vertex. Thus, here too the direct points have a typical vertex. Likewise, there will be a typical arm that addresses the two points. A genuine illustration of a straight pair is a stepping stool that is put against a divider, structures direct points at the ground.
Linearity addresses one that is straight. So here likewise, direct points are the one which is framed into a straight line. The pair of contiguous points here are developed on a line fragment, yet not all nearby points are direct. Thus, we can likewise say, that the direct pair of points is the adjoining points whose non-normal arms are essentially inverse beams.
Explanation for Linear Pair of Angles
At the point when the point between the two lines is 180°, they structure a straight point. A straight point is simply one more approach to address a straight line. A straight line can be imagined as a circle with a limitless range. An A-line section is any bit of a line that has two endpoints. Additionally, a bit of any line with just a single endpoint is known as a beam. A-line section with An and B as two endpoints is addressed as AB. The figure that appeared beneath addresses a line fragment AB and the two bolts toward the end show a line.

If a point O is taken anywhere on the line segment AB as shown, then the angle between the two line segments AO and OB is a straight angle i.e. 180°.
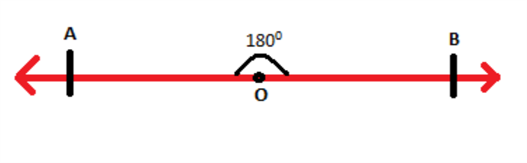
Consider a ray OP bar stand on the line segment AB (bar) as shown:
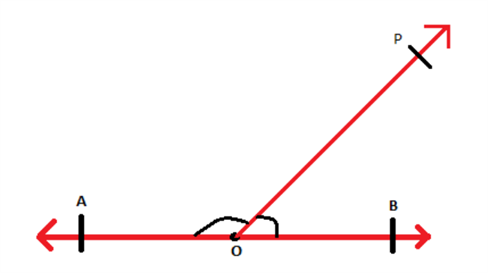
The points which are formed at O are ∠POB and ∠POA. It is realized that the point between the two line portions AO and OB is 180°. thusly, the points ∠POB and ∠POA amount to 180°.
Subsequently, ∠POB + ∠POA = ∠AOB = 180°
∠POB and ∠POA are nearby one another and when the amount of neighboring points is 180° at that point such points structure straight pair of points.
The above conversation can be expressed as an aphorism.
What Are Supplementary Angles?
Two angles are supplementary if their actions amount to 180°. The points don’t need to be close to one another, however! Advantageous sets will consistently be comprised of two right points, or one intense point, and one insensitive point.
At the point when two points’ actions amount to
180∘ , the points are called strengthening (to one another). Beneficial sets can either be comprised of two right points, or one intense and one inhumane point.
angles ABC and DEF are supplementary. We can tell because they’re congruent with angles GHJ and JHI (respectively), and we can tell from the picture that GHJ and JHI add up to make GHI… which is just a straight line (and thus technically has a measure of 180∘.
What is linear pair of angles?
Two angles form a linear pair if they have;
A common arm
A common vertex
Their interiors do not overlap
The sum of two angles is 180°.
Therefore, linear pairs of angles are adjacent angles whose non-common arms are opposite rays.
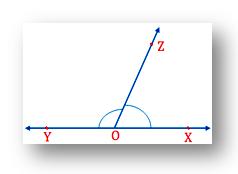
From the above figure, we can notice; OX and OY are two inverse beams and ∠XOZ and ∠YOZ are the adjoining points. Hence, ∠XOZ and ∠YOZ structure a straight pair.
What Is the Linear Pair Postulate?
As indicated by the linear pair postulate, two points that structure a direct pair are valuable. A straight pair is a bunch of neighboring points that structure a line with their unshared beams. At the point when added together, these points equivalent to 180 degrees. This postulate is here and there called the enhancement propose.
Euclid’s Postulates
The Greek mathematician Euclid is perceived as the dad of calculation in light of the commitments he made to the field. His book, “Components,” subtleties 465 hypotheses and verifications that made the establishment of calculation as it’s concentrated today. There are five mathematical hypothesizes clarified in the book.
The main proposal states that it’s feasible to draw a straight line between any two focuses. The second expresses that one can broaden a straight line ceaselessly. Another hypothesis depicts a circle. Another state that okay points are consistent. The fifth hypothesis stays problematic regardless of a few endeavors over the course of the years to demonstrate it.
Postulates vs. Theorems
Proposes are proclamations that have not been demonstrated yet are thought to be valid. For instance, mathematicians accept the assertion “through any two focuses there is actually one line” regardless of the way that it isn’t demonstrated. A hypothesis is a genuine explanation that one can demonstrate. It is feasible to demonstrate the assertion “In the event that two lines cross, they converge in precisely one point.” Both hypotheses and hypotheses can be utilized to demonstrate proclamations identified with math.
Proofs in Geometry
In geometry, the evidence is a contention that affirms or discredits an assertion. The evidence follows the arrangement of realities, derivations, and rationale that help the last end. Hypothesizes like the direct pair propose can be utilized in mathematical verifications and referenced in the avocation part of the confirmation.
Understanding Angles
At the point when two lines, line fragments, or beams meet, they make spaces called points. Mathematicians measure points in degrees, and this estimation characterizes the kind of the point. A straight point (otherwise called a straight line) measures 180 degrees, and a correct point estimates 90 degrees.
The obtuse measure is more noteworthy than 90 degrees. Intense points are under 90 degrees. There are likewise points with a space more prominent than 180 degrees called reflex points. A point arrives at full revolution at 360 degrees. Points can likewise be depicted as sure or negative, contingent upon the heading of the point.
Understanding Lines
Understanding lines is indispensable expertise in the investigation of calculation. A progression of focuses that broaden inconclusively structure a line. Lines don’t have endpoints. They have bolts indicating their limitless nature. A line fragment is essential for a line. Line sections have endpoints, which are focuses along the line. Beams start at a solitary point and broaden endlessly a solitary way.
parallel lines and line portions show side to side in a plane and never converge. Opposite lines cross and structure a 90-degree point at where they meet. These meeting lines are a direct pair since their points equivalent to 180 degrees when added together.
YOUTUBE VIDEO LINK: Linear Pair Postulate - YouTube
How Are Linear Equations Used in Everyday Life?
Variable Costs
Envision that you are taking a taxi while an extended get-away. You realize that the taxi administration charges $9 to get your family from your lodging and another $0.15 per mile for the outing. Without knowing the number of miles it will be to every objective, you can set up a straight condition that can be utilized to discover the expense of any taxi trip you go on your outing. By utilizing “x” to address the number of miles to your objective and “y” to address the expense of that taxi ride, the direct condition would be: y = 0.15x + 9
Rates
LINEAR conditions can be a valuable apparatus for contrasting paces of pay. For instance, on the off chance that one organization offers to pay you $450 each week and different offers $10 each hour, and both request that you work 40 hours out of every week, which organization is offering the better pace of pay? A direct condition can help you sort it out! The primary organization’s offer is communicated as 450 = 40x. The subsequent organization’s offer is communicated as y = 10(40). In the wake of contrasting the two offers, the conditions reveal to you that the principal organization is offering the better pace of pay at $11.25 each hour.
What is the difference between linear pairs and adjacent angles?
Adjacent angles are points that are close to one another for example two points with one regular arm.
All linear pairs are neighboring points however all contiguous points are not direct combines.
linear pair are contiguous points whose whole is equivalent to 180o.
In a linear pair, the arms of the points that are not regular are collinear for example they lie on a straight line.
What is the difference between a linear pair and a pair of supplementary angles?
linear Pairs are an extraordinary subset of advantageous points.
Supplementary Angles are any two points that total 180 degrees.
linear pairs are any two points that share a typical beam and whole to 180 degrees.

How do angles form a linear pair?
linear pair is a couple of adjoining points where the non-normal side structures a straight line Linear pair is a couple of nearby points where the non-regular side structures a linear line Non-Common side (AC) is a straight line. We should take some more models. Do the points frame a linear pair? Thus, points structure a direct pair.
FREQUENTLY ASKED QUESTIONS (FAQs)
Q1. What is the Linear pair theorem?
Actually, it’s the Linear Pair Postulate, which is…
If two angles form a linear pair, then they are supplementary; that is, the sum of their measures is 180 degrees.
Q2. Does a non-linear system obey the superposition theorem?
Any framework that complies with the superposition THEOREM is,
by definition, a linear system.
So a non-straight framework is one that doesn’t comply with the superposition theorems.
Q3. Which of the following reasons can be used for statement 2 of the proof?
vertical angles theorem.
Q4. Are supplementary angles necessarily a linear pair?
No. All linear pair points are beneficial, however, strengthening points don’t need to be a linear pair.
Q5. Is a linear pair is the same as vertical pair?
Not really.
Q6. If two angles form a linear pair then they are complementary true or false?
A linear pair is always supplementary, 180 degrees, not 90.
Q7.Do all supplementary angles form a linear pair Are all linear pairs supplementary?
All supplementary angles don’t shape a linear pair. The contrary points of any quadrilateral recorded all around (a cyclic quadrilateral) are advantageous yet they are not linear pairs. In any case, all linear pairs are beneficial.
Q8. Why do all linear angle pairs must be supplementary but all supplementary angles do not have to be linear pairs?
All supplementary angles would be linear pairs IF they were adjacent. But they could be far apart.
Q9. Which angle pairs add up to 180?
Supplementary Angles.
Q10. What sort of angle is a supplementary angle?
Two angles are supplementary if they add up to 180 degrees. They don’t have to be together, just add up to 180 degrees.