What is Triangle?
A triangle is a three-sided polygon with three vertices and three sides. It is one of the most fundamental geometric shapes. The vertices A, B, and C of a triangle are denoted by. In Euclidean geometry, any three non-collinear points form a unique triangle and, at the same time, a unique plane (i.e. a two-dimensional Euclidean space)
Types of Triangles
A “triangle” is a three-sided polygon with three angles, as the name implies. The number of a triangle’s interior angles will always equal 180 degrees. This is known as the triangle’s angle sum property. A triangle also has a lot of properties. Let’s take a closer look at the different forms of triangles.
There are six types of triangles three are based on the length of the sides: equilateral, isosceles, and scalene. and the rest of the three are based on their Angles: acute, obtuse, right.
Types of Triangles Based on Sides
Triangles are divided into three categories based on the lengths of their sides:
Scalene
Isosceles
Equilateral
Let’s take a look at each one separately.
1.Scalene Triangle
All of the sides of a scalene triangle are of different lengths. In such a triangle, no side would be equal in length to any of the other sides. All of the interior angles in a scalene triangle are also different. A scalene triangle is depicted in the diagram below. As you can see, none of the sides is the same length.

In the figure, you can see that all the sides of the triangle seem to be unequal.
2.Isosceles Triangle
Two of the three sides of an isosceles triangle are similar in length. As a result, the angles opposite the equal sides are equal. An isosceles triangle, in other words, has two equal sides and two equal angles. An isosceles triangle is depicted in the diagram below.

The two sides of the triangle appear to be similar in the diagram above, but the base of the triangle is smaller than the other two sides.
3.Equilateral Triangle
All of the sides of an equilateral triangle are the same length. Each of the interior angles will have a measurement of 60 degrees in this case. An equilateral triangle is also known as an equiangular triangle because its angles are the same. An equilateral triangle is depicted in the diagram below.

All three sides of the triangles are equal in the diagram above, as are all of the interior angles, which are all 60 degrees.
Types of Triangles Based on Angles
In terms of their interior angles, triangles can be divided into three categories:
1.Acute-angle
2.Obtuse-angle
3.Right-angle
Let’s talk about them.
1. Acute Triangle
An acute triangle is one with acute angles on all three interior sides. In other words, an acute-angled triangle is one in which all interior angles are less than 90 degrees. An acute triangle is depicted in the diagram below.

All of the inner angles of the triangle in the above diagram are less than 90 degrees, indicating that it is an acute triangle.
2. Obtuse Triangle
Obtuse triangles have one of the three inner angles with a measurement greater than 90 degrees. In other words, an obtuse-angled triangle is formed when one of the angles in a triangle is an obtuse angle. An obtuse triangle is depicted in the diagram below.

We can see that one of the angles in the triangle above is greater than 90 degrees. As a result, it’s an obtuse triangle.
3. Right Triangle
A right triangle is made up of three angles, one of which is 90 degrees. The longest hand of a right-angled triangle is the hypotenuse, which is the side opposite the right angle (90-degree angle). Triangles with combined names like a right isosceles triangle and others appear, but this only means that the triangle has two equal sides and one of the interior angles is 90 degrees. A right triangle is depicted in the diagram below.
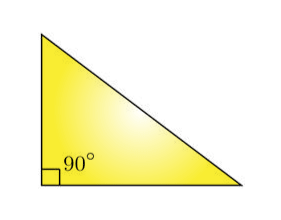
In the above triangle, one among the three angles is 90 degrees, thus it is a right triangle.
YOUTUBE VIDEO LINK: Triangle: Introduction | Learn with BYJU'S - YouTube
EXPLANATION:
In Geometry, a triangle is the main shape, characterized as a shut two-dimensional graph containing 3 sides, 3 points, and 3 vertices. In basic words, a triangle is a polygon with 3 sides. The word triangle is taken from the Latin word ‘triangulus,’ which implies three-cornered.
During antiquated occasions, space experts had made a strategy called triangulation to decide the distances of the far-off stars. They measure the separation from two distinct areas, at that point measure the point made by shift or parallax, framed by the spectator’s development between the two areas. At that point, they used to apply the law of sines for figuring the necessary distance.
The Egyptians made the pyramids around 2900 B.C. Its shape is really that of a 3D pyramid, which has three-sided faces. It is an impeccably designed model that its lengths and points on all sides are something similar. Miletus (624 BC – 547 BC), a Greek mathematician, received Egypt’s calculation and was brought to Greece.
Aristarchus (310 BC – 250 BC), a Greek mathematician, utilized the above technique to discover the distance between the Earth and the Moon. Eratosthenes (276 BC – 195 BC), once more, utilized a similar technique to decide the distance around the outside of Earth (called the circuit).
Properties of Triangle
The properties of triangles have an expansive use. Numerous mathematicians utilized it in taking care of their issues. Euclidean calculation and geometry utilize the properties of triangles.
Here are a couple of essential properties of a triangle:
-
A triangle is a 2-D polygon
-
A triangle has 3 sides, 3 points, and 3 vertices.
-
The amount of lengths of any different sides of a triangle is more than the leftover side’s length.
-
The amount of the length of the three sides gives the border of triangles.
-
The space of a triangle is equivalent to the result of the base and the stature.
Applications of Triangles
LET’S DISCUSS THE APPLICATIONS:
-
Traffic Signs: Most of the traffic signs are shown on three-sided structures.
-
The Pyramids of Egypt: Pyramids are old landmarks built by Egyptians. Pyramids are three-sided fit as a fiddle.
-
Bracket: The supports of rooftops or scaffolds are created in a three-sided shape on the grounds that a triangle is viewed as the most grounded shape.
-
The Bermuda Triangle: The Bermuda Triangle is a three-sided region in the Atlantic Ocean where it is accepted that any boat or airplane that passes at the fact of the matter is gulped. 50 boats and 20 air makes are accepted to have been bafflingly vanished at the Bermuda Triangle.
-
Worldwide Positioning System (GPS) deals with triangulation calculations to decide an item’s longitude and scope.
-
A stepping stool inclining toward a divider makes the state of a triangle.
-
The Eiffel Tower is a three-sided fit as a fiddle.
-
The triangles idea figures the stature or height of tall items, for example, banner posts, mountains, structures, and so on
-
Sandwiches and pizza cuts are three-sided molded.
Special cases of Right Angle Triangles
45-45-90 triangle
In this triangle,
-
Two points measure 45°, and the third point is a correct point.
-
The sides of this triangle will be in the proportion – 1: 1: √2 separately.
-
This is likewise called an isosceles right-calculated triangle since two points are equivalent.
30-60-90 triangle
In this triangle,
This is a right-calculated triangle, since one point = 90°
The points of this triangle are in the proportion – 1: 2: 3, and
The sides inverse to these points will be in the proportion – 1: √3: 2 separately
This is a scalene right-calculated triangle since every one of the three points is extraordinary.
The formula for Area of Triangle
- Area of any triangle = ½ * base * height
- Area of a right-angled triangle = ½ * product of the two perpendicular sides
Summary & Key Takeaways
The amount of all inside points of any triangle is equivalent to 180°
The amount of all outside points of any triangle is equivalent to 360°
An outside point of a triangle is equivalent to the amount of its two inside inverse points
The amount of the lengths of any different sides of a triangle is consistently more prominent than the length of the third side
Essentially, the distinction between the lengths of any different sides of a triangle is in every case not exactly the length of the third side
The side inverse to the littlest inside point is the briefest side and the other way around.
Also, the side inverse to the biggest inside point is the longest side and the other way around.
On account of a right-calculated triangle, this side is known as the hypotenuse
The tallness of a triangle is equivalent to the length of the opposite dropped from a vertex to its contrary side, and this site is viewed as the base
Basic facts
Triangles are thought to be two-dimensional plane figures except if the setting gives in any case (see Non-planar triangles, underneath). In thorough medicines, a triangle is in this way called a 2-simplex (see likewise Polytope). Rudimentary realities about triangles were introduced by Euclid, in books 1–4 of his Elements, composed around 300 BC.
The proportions of the inside points of the triangle consistently amount to 180 degrees (the same tone to call attention to they are equivalent).
The amount of the proportions of the inside points of a triangle in Euclidean space is consistently 180 degrees. This reality is comparable to Euclid’s equal hypothesize. This permits the assurance of the proportion of the third point of any triangle, given the proportion of two points. An outside point of a triangle is a point that is a direct pair (and subsequently strengthening) to an inside point. The proportion of an outside point of a triangle is equivalent to the amount of the proportions of the two inside points that are not contiguous it; this is the outside point hypothesis. The amount of the proportions of the three outside points (one for every vertex) of any triangle is 360 degrees.
Similarity and congruence
Two triangles are supposed to be comparative, if each point of one triangle has a similar measure as the relating point in the other triangle. The relating sides of comparative triangles have lengths that are in a similar extent, and this property is likewise adequate to set up likeness.
Some fundamental hypotheses about comparable triangles are:
In the event that and just on the off chance that one sets of inward points of two triangles have a similar measure as one another, and another pair likewise have similar measure as one another, the triangles are comparative.
In the event that and just on the off chance that one sets of relating sides of two triangles are in similar extent similar to another pair of comparing sides, and their included points have a similar measure, at that point the triangles are comparative. (The included plot for any different sides of a polygon is the inside point between those different sides.)
In the event that and just if three sets of relating sides of two triangles are all in a similar extent, at that point the triangles are similar.[note 3]
Two triangles that are consistent have the very same size and shape:[note 4] all sets of relating inside points are equivalent in measure, and all sets of comparing sides have a similar length. (This is an aggregate of six correspondences, yet three are frequently adequate to demonstrate harmoniousness.)
Some independently important and adequate conditions for a couple of triangles to be harmonious are:
SAS Postulate: Two sides in a triangle have a similar length as different sides in the other triangle, and the included points have a similar measure.
ASA: Two inside points and the remembered side for a triangle have a similar measure and length, separately, like those in the other triangle. (The included side for a couple of points is the side that is basic to them.)
SSS: Each side of a triangle has a similar length as a comparing side of the other triangle.
AAS: Two points and a relating (non-included) side in a triangle have a similar measure and length, separately, similar to those in the other triangle. (This is here and there alluded to as AAcorrS and afterward incorporates ASA above.)
Some independently adequate conditions are:
Hypotenuse-Leg (HL) Theorem: The hypotenuse and a leg in a correct triangle have a similar length as those in another correct triangle. This is likewise called RHS (right-point, hypotenuse, side).
Hypotenuse-Angle Theorem: The hypotenuse and an intense point in one right triangle have a similar length and measure, separately, like those in the other right triangle. This is only a specific instance of the AAS hypothesis.
A significant condition is:
Side-Side-Angle (or Angle-Side-Side) condition: If different sides and a relating non-included point of a triangle have a similar length and measure, individually, similar to those in another triangle, at that point this isn’t adequate to demonstrate consistency; however on the off chance that the point given is inverse to the more drawn outside of the different sides, at that point the triangles are harmonious. The Hypotenuse-Leg Theorem is a specific instance of this standard. The Side-Side-Angle condition doesn’t without anyone else ensure that the triangles are harmonious in light of the fact that one triangle could be coldhearted calculated and the other intense calculated.
Utilizing right triangles and the idea of comparability, the mathematical capacities sine and cosine can be characterized. These are elements of a point that are researched in geometry.
Right triangles
A focal hypothesis is a Pythagorean hypothesis, which states in any correct triangle, the square of the length of the hypotenuse rises to the amount of the squares of the lengths of the two different sides. On the off chance that the hypotenuse has length c, and the legs have lengths an and b, at that point the hypothesis expresses that
{\displaystyle a^{2}+b^{2}=c^{2}.}{\displaystyle a^{2}+b^{2}=c^{2}.}
The opposite is valid: if the lengths of the sides of a triangle fulfill the above condition, at that point the triangle has a correct point inverse side c.
Some different realities about right triangles:
The intense points of a correct triangle are corresponding.
{\displaystyle a+b+90^{\circ }=180^{\circ }\Rightarrow a+b=90^{\circ }\Rightarrow a=90^{\circ }-b.}{\displaystyle a+b+90^{\circ }=180^{\circ }\Rightarrow a+b=90^{\circ }\Rightarrow a=90^{\circ }-b.}
Assuming the legs of a correct triangle have a similar length, the points inverse those legs have a similar measure. Since these points are corresponding, it follows that each actions 45 degrees. By the Pythagorean hypothesis, the length of the hypotenuse is the length of a leg times √2.
In a correct triangle with intense points estimating 30 and 60 degrees, the hypotenuse is double the length of the more limited side, and the more drawn out side is equivalent to the length of the more limited side occasions √3:
{\displaystyle c=2a,}c=2a,
{\displaystyle b=a\times {\sqrt {3}}.}b=a\times {\sqrt {3}}.
For all triangles, points and sides are connected by the law of cosines and the law of sines (likewise called the cosine rule and sine rule).
EXISTENCE OF TRIANGLE
Condition on the sides
The triangle imbalance expresses that the amount of the lengths of any different sides of a triangle should be more noteworthy than or equivalent to the length of the third side. That aggregate can rise to the length of the third side just on account of a savage triangle, one with collinear vertices. It isn’t feasible for that whole to be not exactly the length of the third side. A triangle with three given positive side lengths exists if and just if those side lengths fulfill the triangle imbalance.
Conditions on the angles
Three given points structure a non-degenerate triangle (and to be sure endlessness of them) if and just if both of these conditions hold: (a) every one of the points is positive, and (b) the amount of the points to 180°. On the off chance that degenerate triangles are allowed, points of 0° are allowed.
Points, lines, and circles associated with a triangle
There are a huge number of various developments that track down an uncommon point related with (and regularly inside) a triangle, fulfilling some interesting property: see the article Encyclopedia of Triangle Centers for a list of them. Regularly they are developed by discovering three lines related in an even manner with the three sides (or vertices) and afterward demonstrating that the three lines meet in a solitary point: a significant device for demonstrating the presence of these is Ceva’s hypothesis, which gives a standard for deciding when three such lines are simultaneous. Additionally, lines related to a triangle are regularly built by demonstrating that three evenly developed focuses are collinear: here Menelaus’ hypothesis gives a valuable general model. In this part, only a couple of the most usually experienced developments are clarified.
The circumcenter is the focal point of a circle going through the three vertices of the triangle.
An opposite bisector of a side of a triangle is a straight line going through the midpoint of the side and being opposed to it, for example framing a correct point with it. The three opposite bisectors meet in a solitary point, the triangle’s circumcenter, ordinarily indicated by O; this point is the focal point of the circumcircle, the circle going through every one of the three vertices. The width of this circle, called the circumdiameter, can be found from the law of sines expressed previously. The circumcircle’s range is known as the circumradius.
Thales’ hypothesis infers that assuming the circumcenter is situated on a side of the triangle, the contrary point is a correct one. Assuming the circumcenter is situated inside the triangle, the triangle is intense; on the off chance that the circumcenter is situated externally the triangle, the triangle is heartless.
A height of a triangle is a straight line through a vertex and opposite to (for example shaping a correct point with) the contrary side. This contrary side is known as the base of the elevation, and where the height crosses the base (or its expansion) is known as the foot of the height. The length of the height is the distance between the base and the vertex. The three heights converge in a solitary point, called the orthocenter of the triangle, ordinarily meant by H. The orthocenter lies inside the triangle if and just if the triangle is intense.
The crossing point of the point bisectors is the focal point of the incircle.
A point bisector of a triangle is a straight line through a vertex that slices the comparing point down the middle. The three-point bisectors cross in a solitary point, the incenter, as a rule, indicated by me, the focal point of the triangle’s incircle. The incircle is the circle which lies inside the triangle and contacts every one of the three sides. Its range is known as the inradius. There are three other significant circles, the excircles; they lie outside the triangle and contact one side just as the augmentations of the other two. The focuses of the in-and excircles structure an orthocentric framework.
The middle of a triangle is a straight line through a vertex and the midpoint of the contrary side, and partitions the triangle into two equivalent regions. The three medians meet in a solitary point, the triangle’s centroid or mathematical barycenter, ordinarily signified by G. The centroid of an inflexible three-sided object (cut out of a slender sheet of uniform thickness) is likewise its focal point of mass: the article can be adjusted on its centroid in a uniform gravitational field. The centroid cuts each middle in the proportion 2:1, for example, the distance between a vertex and the centroid is double the distance between the centroid and the midpoint of the contrary side.
A nine-point circle exhibits an evenness where six focuses lie on the edge of the triangle.
The midpoints of the three sides and the feet of the three heights all lie on a solitary circle, the triangle’s nine-point circle. The leftover three focuses for which it is named are the midpoints of the segment of height between the vertices and the orthocenter. The span of the nine-point circle is a large portion of that of the circumcircle. It contacts the incircle (at the Feuerbach point) and the three excircles.
The orthocenter (blue point), the focal point of the nine-point circle (red), centroid (orange), and circumcenter (green) all lie on a solitary line, known as Euler’s line (red line). The focal point of the nine-point circle lies at the midpoint between the orthocenter and the circumcenter, and the distance between the centroid and the circumcenter is a large portion of that between the centroid and the orthocenter.
The focal point of the incircle isn’t overall situated on Euler’s line.
In the event that one mirrors a middle in the point bisector that goes through a similar vertex, one gets a symmedian. The three symmedians converge in a solitary point, the symmedian point of the triangle.
Triangles in construction
rectangle shapes have been the most famous and normal mathematical structure for structures since the shape is not difficult to stack and coordinate; as a norm, it is not difficult to plan furniture and apparatuses to fit inside rectangularly formed structures. However, triangles, while more hard to utilize thoughtfully, give a lot of solidarity. As PC innovation assists engineers with planning inventive new structures, three-sided shapes are getting progressively pervasive as parts of structures and as the essential shape for certain kinds of high rises just as building materials. In Tokyo in 1989, designers had puzzled over whether it was feasible to fabricate a 500-story pinnacle to give moderate office space to this thickly pressed city, yet with the threat to structures from tremors, engineers thought about that as a three-sided shape would be essential if such a structure were to be built.
In New York City, as Broadway jumbles significant roads, the subsequent squares are cut like triangles, and structures have been based on these shapes; one such structure is the geometrically formed Flatiron Building which land individuals concede has a “warren of abnormal spaces that don’t effectively oblige current office furniture” however that has not kept the construction from turning into a milestone icon. Designers have made houses in Norway utilizing three-sided themes. Triangle shapes have shown up in churches just as open structures including colleges just as supports for imaginative home designs.
Triangles are tough; while a square shape can fall into a parallelogram from strain to one of its focuses, triangles have a characteristic strength that supports structures against horizontal pressing factors. A triangle won’t change shape except if its sides are twisted or broadened or broken or if its joints break; generally, every one of the three sides upholds the other two. A square shape, interestingly, is more subject to the strength of its joints from a primary perspective. Some inventive planners have proposed making blocks not out of square shapes, yet with three-sided shapes which can be joined in three dimensions. It is likely that triangles will be utilized progressively in new manners as engineering expansions in intricacy. Recollect that triangles are solid as far as inflexibility, however, while stuffed in a decorating game plan triangles are not as solid as hexagons under pressure (henceforth the commonness of hexagonal structures in nature). Decorated triangles actually keep up predominant strength for cantilevering, nonetheless, and this is the reason for one of the most grounded man-made designs, the tetrahedral bracket.
FREQUENTLY ASKED QUESTIONS
Q1.What are the four types of triangles?
These four sorts of triangles; right, scalene, symmetrical, and isosceles. I tried four of my forecasts by utilizing math. I anticipated that the cheddar was a correct triangle and I was right. For a triangle to be a correct point it must have a hypotenuse and a leg while additionally having a 90-degree point.
Q2.How are the sides of a triangle classified?
In the above triangle, one among the three points is 90 degrees, hence it is a correct triangle. Record the kinds of triangles grouped dependent on their sides. Notice the grouping of a triangle dependent on its point. Characterize scalene, isosceles and symmetrical triangle. In a scalene triangle, every one of the sides of a triangle is of various lengths.
Q3.What is the name of a triangle with two sides?
Isosceles: signifies “equivalent legs”, and we have two legs, isn’t that so? Additionally I SOS has two equivalent “Sides” joined by an " Odd" side. Scalene: signifies “lopsided” or “odd”, so no equivalent sides. What Type of Angle? Triangles can likewise have names that mention to you what sort of point is inside:
Q4.How are the sides of a triangle of equal length?
In a symmetrical triangle, every one of the sides of a triangle is of equivalent length. Characterize intense, harsh, and right triangle. In an intense triangle, every one of the points of a triangle is under 90 degrees. In an uncaring triangle, one of the points of a triangle is more prominent than 90 degrees.
Q5.What kind of triangle has all 3 sides unequal?
A triangle where each of the 3 sides is inconsistent and anybody’s point is a correct point is known as a privilege scalene triangle. A triangle that has one vertex point as heartless and every one of the 3 sides measures diversely is called an insensitive scalene triangle.
Q6.How many angles are there in a triangle?
Thus, essentially, a triangle is a shut mathematical shape that has three points, three sides, and three vertices. The amount of the three points of a triangle is 180°. Allow us currently to investigate the various kinds of triangles.
Q7.How are the different types of triangles classified?
Record the sorts of triangles ordered dependent on their sides. Notice the order of a triangle dependent on its point. Characterize scalene, isosceles and symmetrical triangle. In a scalene triangle, every one of the sides of a triangle is of various lengths. In an isosceles triangle, different sides of a triangle are of a similar measure.
Q8.What are triangles in geometry?
What are Triangles in Geometry? In Geometry, triangles are the kind of polygons, which have three sides and three vertices. This is a two-dimensional figure with three straight sides. A triangle is viewed as a 3-sided polygon. The amount of the relative multitude of three points of a triangle is equivalent to 180°. The triangle is contained in a solitary plane.
Q9. Define scalene, isosceles and equilateral triangle.
In a scalene triangle, every one of the sides of a triangle is of various lengths. In an isosceles triangle, different sides of a triangle are of a similar measure. In a symmetrical triangle, every one of the sides of a triangle is of equivalent length.
Q10. Can an acute triangle be a scalene triangle?
An intense triangle can be a scalene triangle, isosceles triangle, or symmetrical triangle. The intense triangle can be drawn if the triangle has equivalent or inconsistent side lengths.
CONCLUSION
I anticipated that the cheddar was a correct triangle and I was right. For a triangle to be a correct point it must have a hypotenuse and a leg while likewise having a 90-degree point. The cheddar satisfied those prerequisites as it had a hypotenuse, leg, and had a 90-degree point. For the scalene triangle I said a slice of Kroger bread was a scalene triangle since when you took a gander at it, it looked like no sides or points were harmonious with one another. I was directly on that reality as I demonstrated the triangle scalene. I took a gander at all of the estimations of each side and none of them was something very similar. None of the points were compatible either demonstrating that the triangle is scalene. For the symmetrical triangle, I picked a wheat wafer and I wasn’t right. I picked the wheat wafer since the entirety of the sides and points appeared to be identical yet I wasn’t right. The sides were off by somewhat however the points were right. Despite the fact that my points were all consistent for it to be an asymmetrical triangle everything must be something similar. For the isosceles I picked cheddar I found at the store since two of the sides and points looked consistent. For it to be an isosceles triangle 2 of the sides must be something very similar. At the point when I figured it out it didn’t work out as it was off on the estimations. This undertaking showed me how the eye isn’t in every case right yet, in addition, instructed me that there are a ton of triangles in regular daily existence.